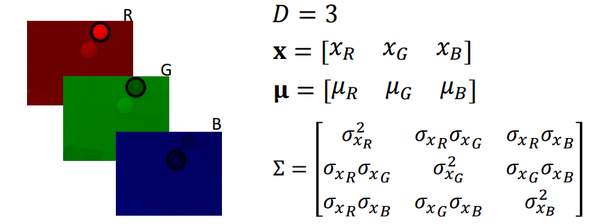3 most important points
- 贝叶斯定理P(H∣E)=P(E)P(H)⋅P(E∣H)=P(H)P(E∣H)+P(¬H)P(E∣¬H)P(H)⋅P(E∣H)
- 一元高斯分布p(x)=2πσ1e−2σ2(x−μ)2
最大似然估计求解 μ^=N1∑i=1Nxi, σ^2=N1∑i=1N(xi−μ^)2
- 所有分布都可以表示为多个高斯分布叠加,因此混合高斯模型可以用来建模任意特征;使用EM算法可以求解GMM,其中E为“Expectection”,对不同单高斯分布的权重进行预测,M为“Maximization”,更新每一个单高斯分布
5 thoughts
- 贝叶斯因子是区别于“似然比”的一种估计方法
- 如何对矩阵进行求导?
- 需要自己动手进行一次EM算法的实现,或者了解在python中如何实现EM算法
- 需要了解一些贝叶斯定理的实际应用
Notes
贝叶斯定理
- 贝叶斯定理
- 核心:新证据不能直接凭空的决定你的看法,而是应该更新你的先验看法(经验)
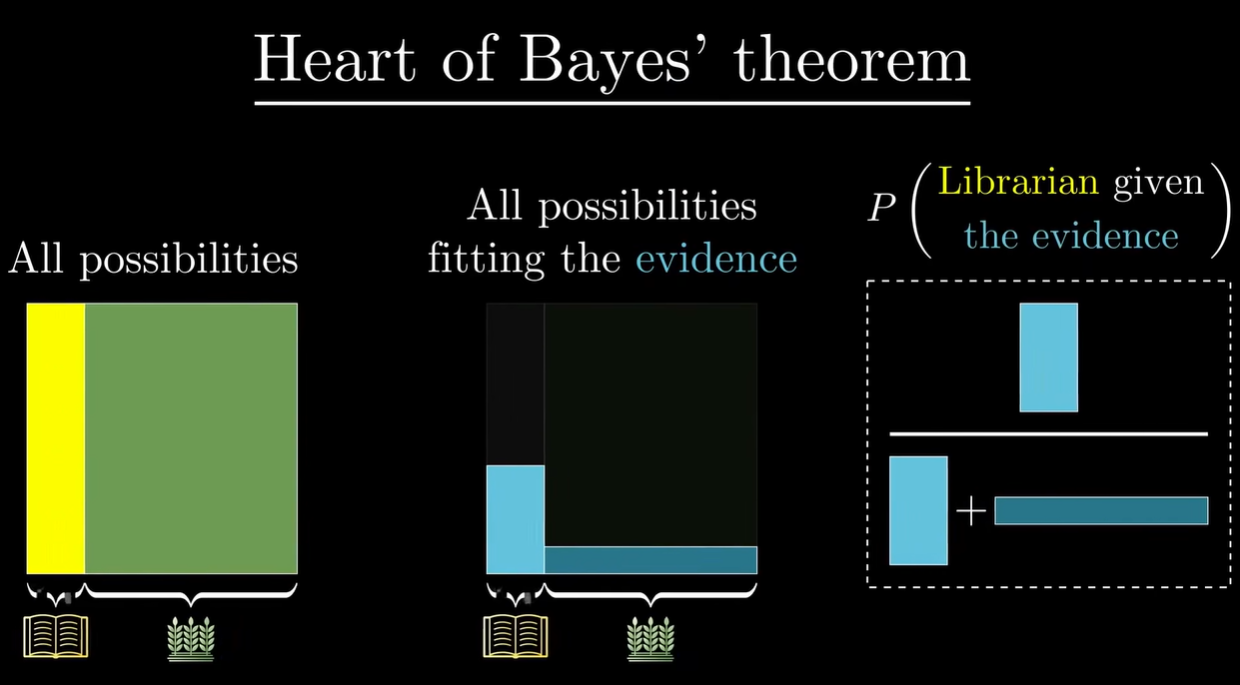 例如,描述一个文静的人,你觉得 ta 更可能是图书管理员还是农民?
例如,描述一个文静的人,你觉得 ta 更可能是图书管理员还是农民?
- 场景:给定假设和证据,你想知道在证据为真的条件下假设成立的概率
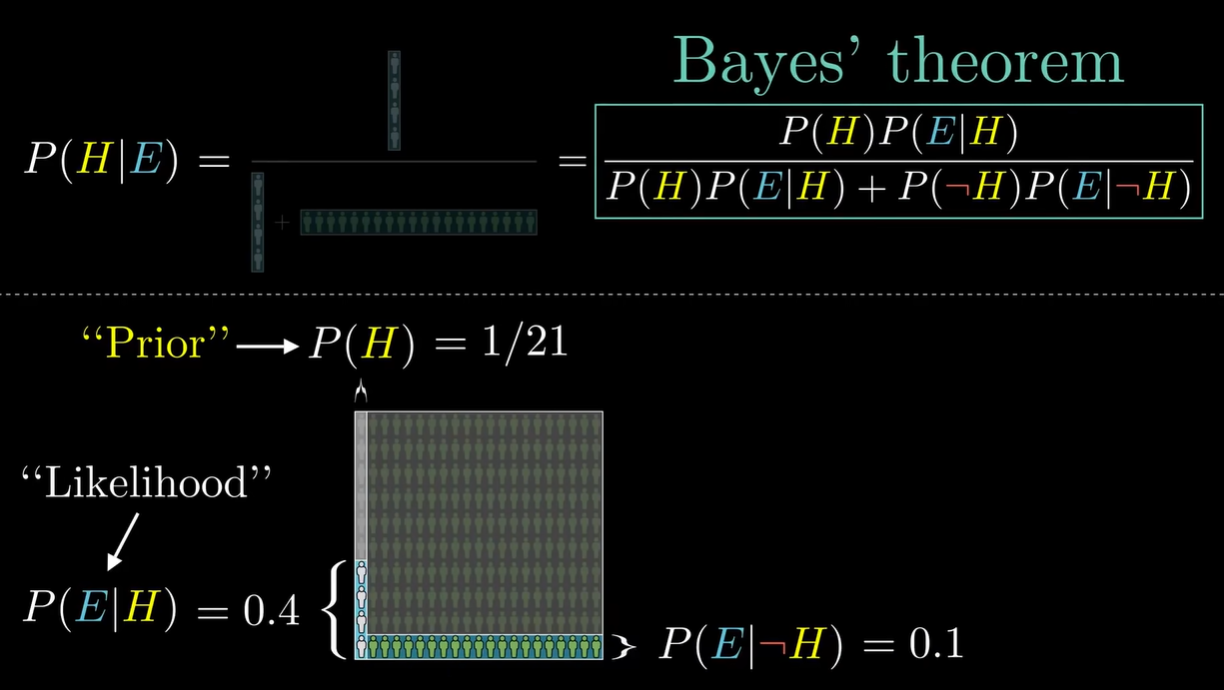
- @ 公式:P(H∣E)=P(E)P(H)⋅P(E∣H)=P(H)P(E∣H)+P(¬H)P(E∣¬H)P(H)⋅P(E∣H)
- P(H∣E):后验概率,posterior Hypothesis given the evidence
- P(H):先验概率,prior 就是在不考虑证据的情况下,假设成立的概率
- P(E∣H):似然概率,likelihood 假设成立时,其中符合证据描述的比例
- P(E):假设成立的概率
- 证明:
- 可视化:
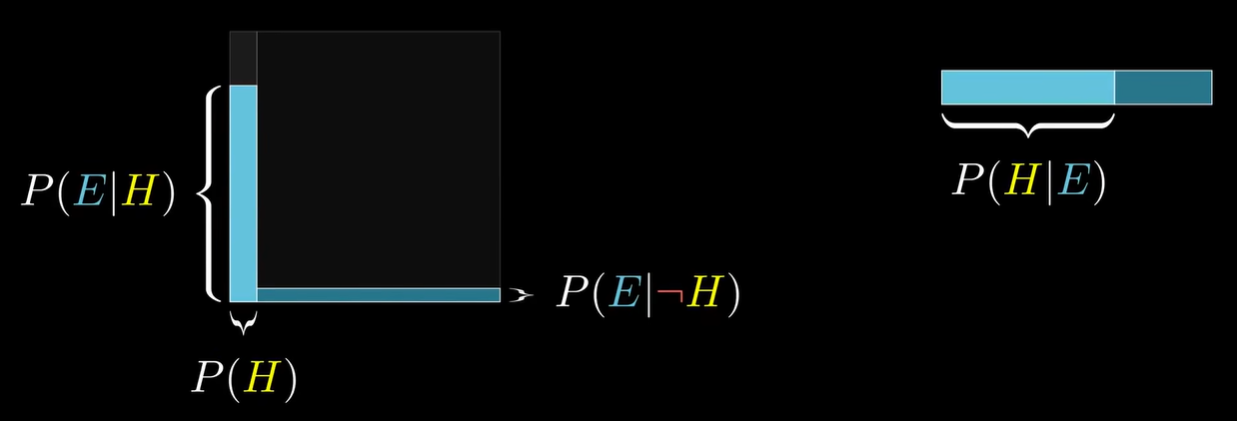
- 补充:
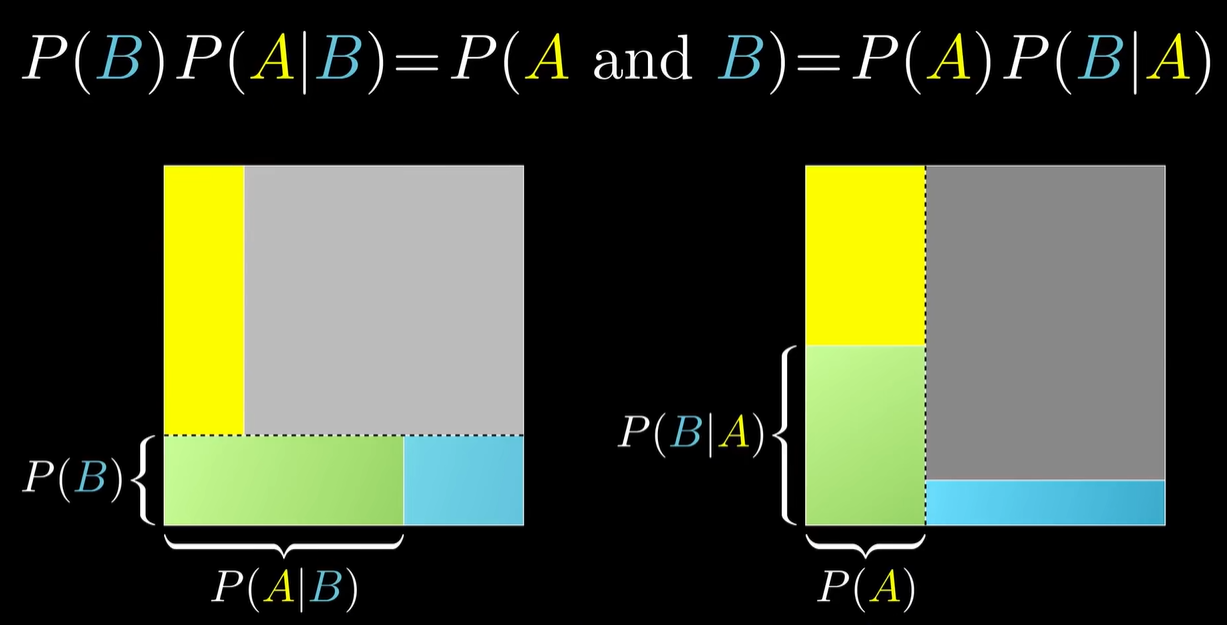
- 这是另一种视角,说明贝叶斯定理成立的原因;上述等式可通过移项得到贝叶斯定理
- 另一方面,P(A and B)=P(B)P(A∣B) 这样的式子指出了一个常见的误区:大部分情况下,事件 A 和 B 不是相互独立的;只有当二者独立的时候,P(A and B)=P(A)P(B) 成立,这是因为 P(A∣B)=P(A)
- 贝叶斯因子
- 定义:

- 比较:

- 比率和概率是两种不同的表达,比如:
1:1 = 50% 或者 4:1 = 20%
- 通过贝叶斯因子,能够更快地估计概率
- 这只是一种估计方法,当先验概率比较小的时候可以使用
- 二项分布
- 引入:购物时,查看好评率的时候会考虑样本数量;当样本量大的时候,人们更倾向于相信,而样本量小的时候会有所顾虑
 运用拉普拉斯平滑方法,在已有数据上加上一个好评和一个差评,即人们心中的结果
运用拉普拉斯平滑方法,在已有数据上加上一个好评和一个差评,即人们心中的结果
- 可视化:概率的概率
- 情景:购物时,在所有人在该商家购物体验好的概率(s)的基础上知道自己能体验好的概率(p),其中 s 是不固定的
- 问题:在现实生活中,不能从已有的数据得到一个“恒定频率”(如骰子、硬币展现的),只有一个“估计”——测试不能保证真正的概率
- 建模:P(data∣s)→P(s∣data)
注意这里前后两个 s 不是一回事儿,后一个 s 可能实际上指的是情景中的 p
- 定义:单次随机事件只有两种可能的结果,重复某个次数之后,得到某种组合的概率
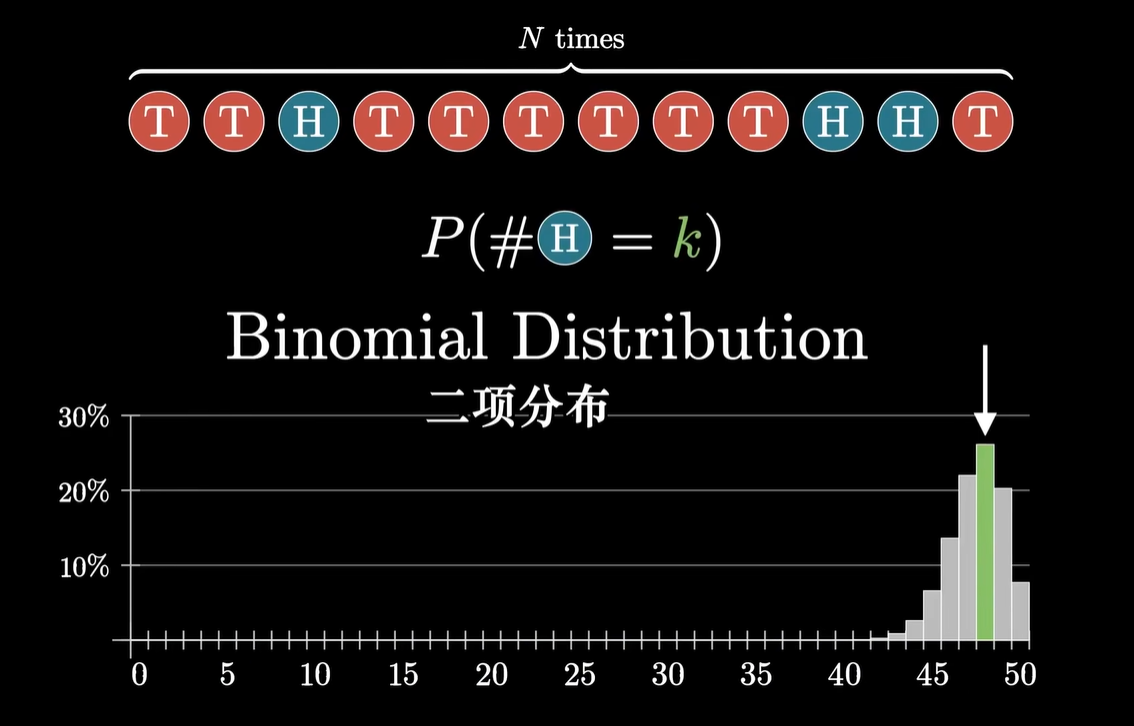
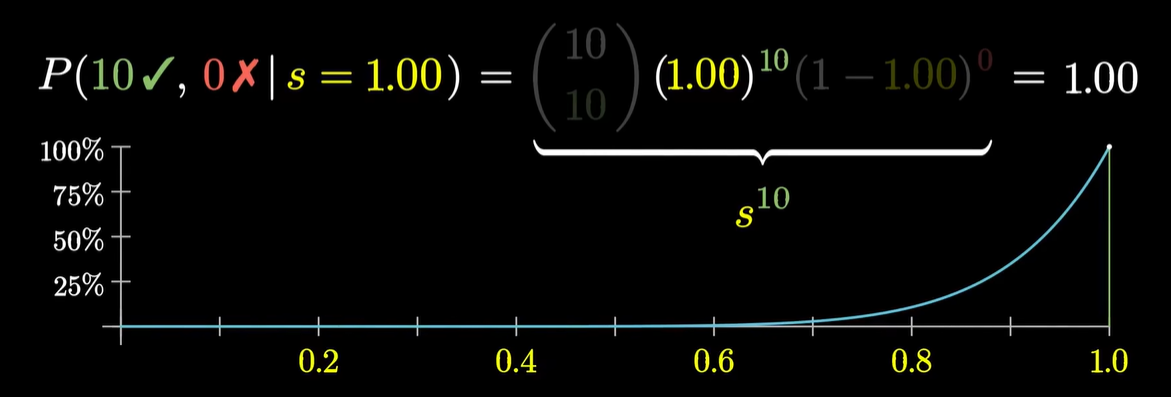
- ~ 计算:P(data∣s)=c⋅s#✓(1−s)#✘;其中 c 为组合数,比如说 C108*
- 问题:当所求组合为全对,当 s 接近 1 的时候最可能实现,但是显然 s 不可能是 1
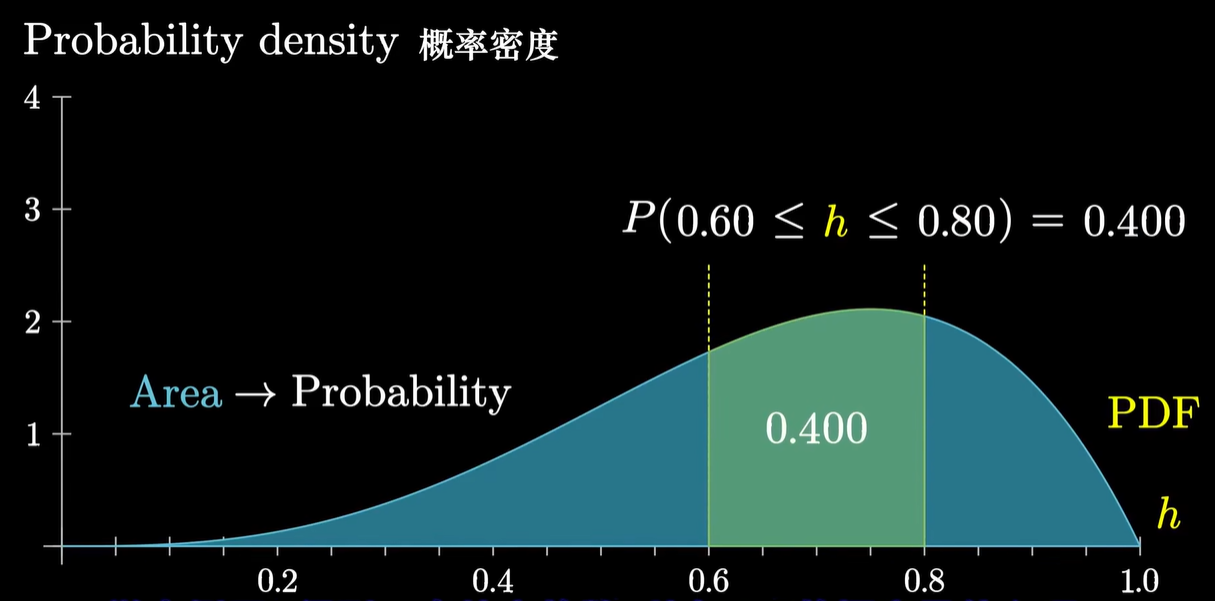
- 概率密度函数 Porbability Density Function (PDF)
- 场景:处理连续变化的概率,需要积分;就像处理离散的概率需要相加
- 定义:
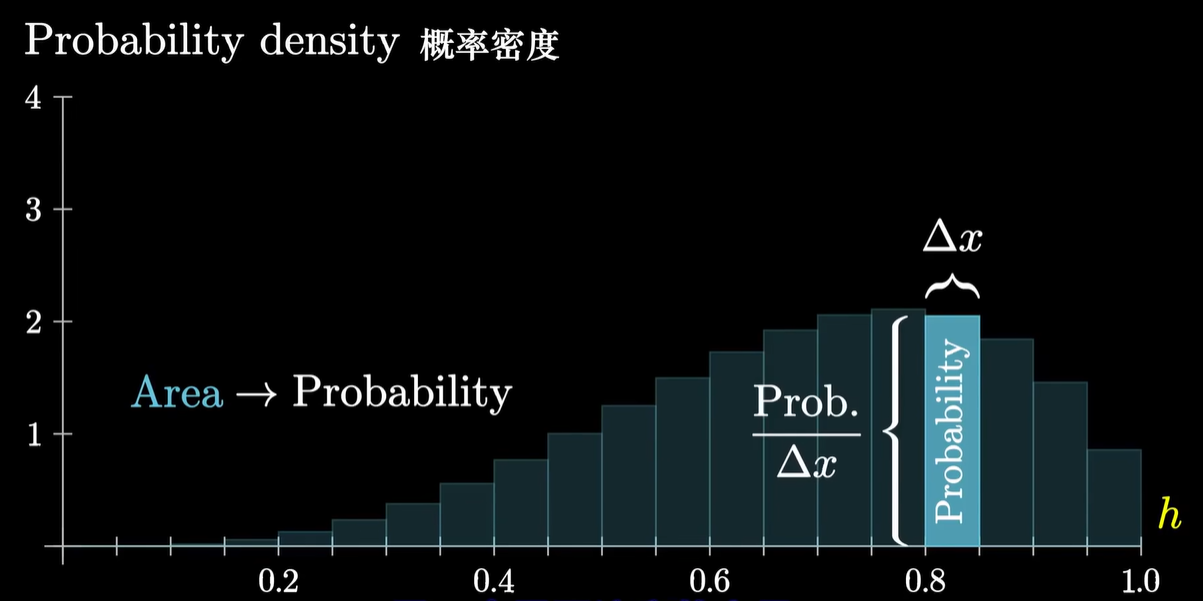
- 性质:曲线下面积和为1
- 意义:一个随机变量出现在两个值区间的概率
高斯分布
一元高斯分布
- 高斯分布
- 定义:高斯分布,也叫正态分布,是最常见的连续概率分布之一。它的概率密度函数呈对称的钟形曲线,完全由两个参数决定:
- 均值 μ:决定分布的中心位置。
- 标准差 σ:决定曲线的“胖瘦”,σ 越大,数据越分散。
- @ 概率密度函数:p(x)=2πσ1e−2σ2(x−μ)2
- 特性:
- 对称性:均值处概率最高,左右对称。
- 68-95-99.7 规则:约 68% 的数据落在 μ±σ 内,95% 在 μ±2σ,99.7% 在 μ±3σ。
- 中心极限定理:大量独立随机变量的均值趋近高斯分布,这也是它在统计学和机器学习中广泛应用的原因。
- 举例:检测图片中的黄色小球
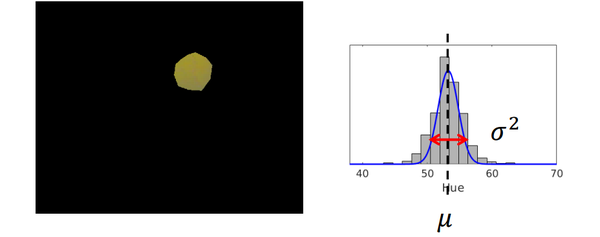 横轴代表每个像素,但是记录每个像素非常消耗存储空间,考虑用高斯分布来拟合
横轴代表每个像素,但是记录每个像素非常消耗存储空间,考虑用高斯分布来拟合
- 最大似然估计(Maximum Likelihood Estimation,MLE)
- 用途:求解高斯分布
- 似然 Likelihood
- 定义:在给定模型参数的情况下观测值出现的概率,即条件概率 p({xi}∣μ,σ)
- 举例:比如,在上一节的小球例子中,{xi} 表示所有“黄色”像素点的色相值,如果给定了高斯分布的 μ 和 σ,我们就能算出 {xi} 出现的概率。
- ~ 结论:μ^=N1∑i=1Nxi, σ^2=N1∑i=1N(xi−μ^)2
- 证明:
- 问题定义:给定观测值 {xi},求 μ 和 σ 使得似然函数最大 μ^,σ^=arg μ,σmax p({xi}∣μ,σ)
其中 μ^,σ^ 表示估计值
- {xi} 是观测值的集合,假设这些观测值相互独立(在例子中是这样的),则 p({xi}∣μ,σ)=∏i=1Np(xi∣μ,σ)
代入问题,得到目标:μ^,σ^=arg μ,σmax ∏i=1Np(xi∣μ,σ)
- 根据对数函数的单调性,对右式求最大值等价于对右式取对数再求最大值,可将连乘展开为相加:\begin{align} \hat{\mu},\hat{\sigma} &=\text{arg}\ \underset{\mu,\sigma}{\max}\ln{ \{\prod_{i=1}^Np(x_i|\mu,\sigma)} \}\\ &=\text{arg}\ \underset{\mu,\sigma}{\max}\sum_{i=1}^{N}\ln p(x_i|\mu,\sigma) \end{align}
- 显然 p(xi∣μ,σ) 是即为高斯分布上的一个点,可以代入概率密度函数求解:\begin{align} \ln p(x_i|\mu,\sigma) &= \ln ( \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x_i-\mu)^2}{2\sigma^2}} ) \\ &= -\frac{(x_i-\mu)^2}{2\sigma^2}-\ln\sigma-\ln\sqrt{2\pi} \end{align}
- 而常数项对求最值没有影响,所以最终目标可以化成:\begin{align} \hat{\mu},\hat{\sigma} &= \text{arg}\ \underset{\mu,\sigma}{\max}\sum_{i=1}^{N} (-\frac{(x_i-\mu)^2}{2\sigma^2}-\ln\sigma-\ln\sqrt{2\pi}) \\ &= \text{arg}\ \underset{\mu,\sigma}{\max}\sum_{i=1}^{N} (-\frac{(x_i-\mu)^2}{2\sigma^2}-\ln\sigma) \\ &= \text{arg}\ \underset{\mu,\sigma}{\min}\sum_{i=1}^{N} (\frac{(x_i-\mu)^2}{2\sigma^2}+\ln\sigma) \end{align}
- 求最值当然是要求导啦,所以对目标函数 J(μ,σ) 求偏导:\begin{align} \frac{\partial J}{\partial \mu} &= \sum_{i=1}^N\frac{-2(x_i-\mu)}{2\sigma^2}\\ &=\frac{1}{\sigma^2}(N\mu-\sum_{i=1}^Nx_i)\\ &=0 \end{align}
求得:μ^=N1∑i=1Nxi
- 带回目标函数得到 J′(σ),再次求导:\begin{align} \frac{d J'(\sigma)}{d \sigma} &=\frac{N}{\sigma} - \sum_{i=1}^N\frac{(x_i-\mu)^2}{\sigma^3} \\ &= \frac{1}{\sigma}(N-\frac{1}{\sigma^2}\sum_{i=1}^N(x_i-\hat\mu)^2)\\ &=0 \end{align}
求得:σ^2=N1∑i=1N(xi−μ^)2
多元高斯分布
- 多元高斯分布
- @ 概率密度函数:p(x)=(2π)D/2∣Σ∣1/21exp{−21(x−μ)TΣ−1(x−μ)}
其中 D 表示维度(元的数目),x 是一个向量
Σ 表示协方差矩阵,∣Σ∣ 表示 Σ 的行列式值
- 协方差矩阵 Covariance Matrix
- 定义:协方差矩阵是一个方阵,由两部分组成,方差(Variance)和相关性(Correlation),对角线上的值表示方差,非对角线上的值表示维度之间的相关性。
- 举例:Σ=[σx12σx2σx1σx1σx2σx22](σx1σx2=σx2σx1)
- 举例:检测图片中的黄色小球(RGB版)
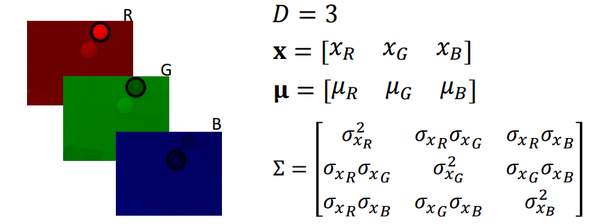
- 最大似然估计(多元高斯分布版)
- ~ 结论:μ^=N1∑i=1Nxi, Σ^=N1∑i=1N(xi−μ^)(xi−μ^)T
- 证明:
- 和求解一元高斯分布类似,将问题描述为:给定观测值 {xi},求 μ 和 Σ,使得似然函数最大:μ^,Σ^=arg μ,Σmax p({xi}∣μ,Σ)
- 经过取对数、代入、化为和等一系列操作,得到目标函数:J(μ,Σ)=∑i=1N(21(xi−μ)TΣ−1(xi−μ)+21ln∣Σ∣)
- 接着求偏导:\begin{align}
\frac{\partial J}{\partial \boldsymbol\mu}
&= \frac{\partial}{\partial\boldsymbol\mu}\sum_{i=1}^N(\frac{1}{2}(\boldsymbol{x_i}-\boldsymbol\mu)^T\Sigma^{-1}(\boldsymbol{x_i}-\boldsymbol\mu)+\frac{1}{2}|\Sigma|)
\\&=
\frac{\partial}{\partial\boldsymbol\mu}\frac{1}{2}\sum_{i=1}^N(\boldsymbol{x_i}^T\Sigma^{-1}\boldsymbol{x_i}-\boldsymbol{x_i}^T\Sigma^{-1}\boldsymbol\mu-\boldsymbol\mu^T\Sigma^{-1}\boldsymbol{x_i}+\boldsymbol\mu^T\Sigma^{-1}\boldsymbol\mu)
\\&=
\frac{\partial}{\partial\mu}\sum_{i=1}^N(\frac{1}{2}\boldsymbol\mu^T\Sigma^{-1}\boldsymbol\mu-\boldsymbol\mu\Sigma^{-1}\boldsymbol{x_i})
\\&=
\Sigma^{-1}\sum_{i=1}^N(\boldsymbol\mu-\boldsymbol{x_i})
\\&=
\boldsymbol{0}
\end{align} \begin{align}
\frac{\partial J}{\partial\Sigma}
&=\frac{\partial}{\partial\Sigma}\sum_{i=1}^N(\frac{1}{2}(\boldsymbol{x_i}-\hat{\boldsymbol\mu})^T\Sigma^{-1}(\boldsymbol{x_i}-\hat{\boldsymbol\mu})+\frac{1}{2}\ln|\Sigma|)
\\&=
\frac{1}{2}\sum_{i=1}^N(-\Sigma^{-1}(\boldsymbol{x_i}-\hat{\boldsymbol\mu})(\boldsymbol{x_i}-\hat{\boldsymbol\mu})^T\Sigma^{-1}+\Sigma^{-1})
\\&=
\frac{1}{2}\Sigma^{-1}(-(\sum_{i=1}^N(\boldsymbol{x_i}-\hat{\boldsymbol\mu})(\boldsymbol{x_i}-\hat{\boldsymbol\mu})^T)\Sigma^{-1}+N\boldsymbol{I})
\\&=
\boldsymbol{0}
\end{align}
- 求得:μ^=N1∑i=1Nxi, Σ^=N1∑i=1N(xi−μ^)(xi−μ^)T
混合高斯模型
- 混合高斯模型(Gaussian Mixture Model,GMM)
- 实际:多个单高斯模型的和,任何分布都可以用 GMM 来表示
- 概率密度函数:p(x)=∑k=1Kwkgk(x∣μk,Σk)
- 其中 gk 是均值为 μk,协方差矩阵为 Σk 的单高斯模型,
- wk 是 gk 的权重系数,wk>0,∑k=1Kwk=1,
- K 是单高斯模型的个数
- 优点:能够表示任何分布
- 缺点:
- 参数过多,求解复杂
- 对观测值建模效果过好容易过拟合
- 最大期望算法(Expectation Maximization algorith,EM)
- 思想:由于GMM过于复杂,没有解析解,所以通过迭代的方法逼近最优解
- 步骤:

- 猜测一个初始解(不同初值会得到不同的解)
- E-step:引入中间变量zki=∑i=1Kgk(xi∣μk,Σk)gk(xi∣μk,Σk)(k=1,2,⋯,K; i=1,2,⋯,N)可以理解为每个单高斯分布对每个位置 i 的权重
- M-step:zk=∑i=1Nzki 可以理解为第 k 个单高斯分布对整个GMM的贡献,在更新 zki 之后,反过来用它更新每一个单高斯分布:\begin{align}
& \boldsymbol\mu_k = \frac{1}{z_k}\sum_{i=1}^Nz_k^i\boldsymbol{x_i} \\
& \Sigma_k = \frac{1}{z_k}\sum_{i=1}^Nz_k^i(\boldsymbol{x_i}-\boldsymbol\mu_k)(\boldsymbol{x_i}-\boldsymbol\mu_k)^T
\end{align}
- 循环更新,当相邻两个步骤值的差小于 threshold 时,得到结果
微积分
Reference
概率论
高斯分布
 例如,描述一个文静的人,你觉得 ta 更可能是图书管理员还是农民?
例如,描述一个文静的人,你觉得 ta 更可能是图书管理员还是农民?
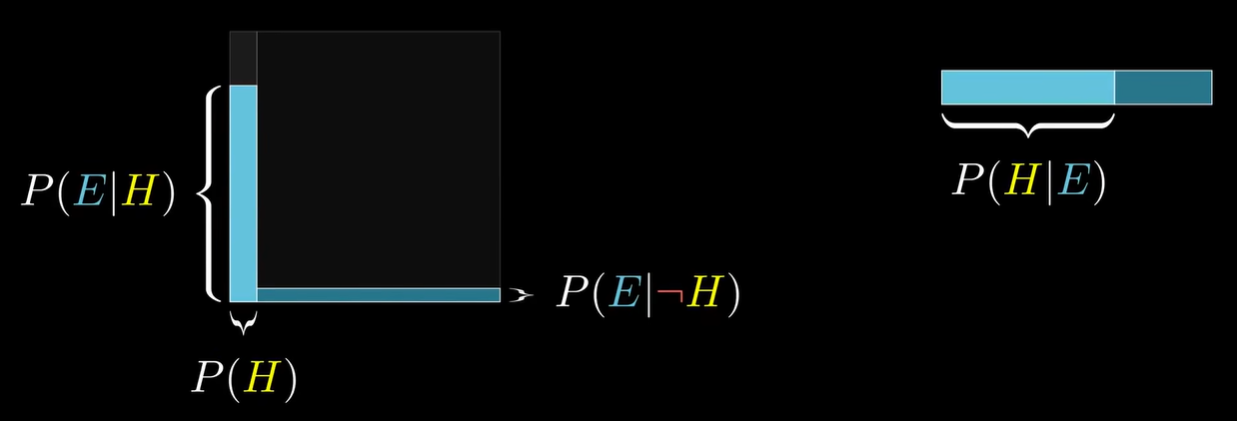
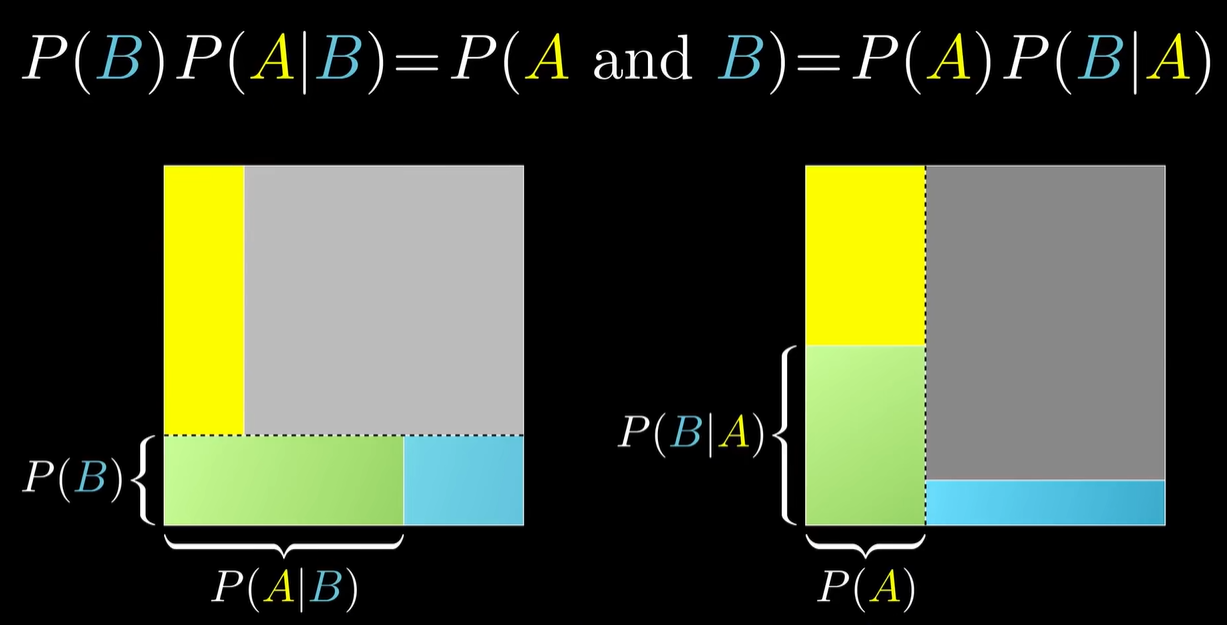


 运用拉普拉斯平滑方法,在已有数据上加上一个好评和一个差评,即人们心中的结果
运用拉普拉斯平滑方法,在已有数据上加上一个好评和一个差评,即人们心中的结果



 横轴代表每个像素,但是记录每个像素非常消耗存储空间,考虑用高斯分布来拟合
横轴代表每个像素,但是记录每个像素非常消耗存储空间,考虑用高斯分布来拟合