3 most important points
- 微积分基本定理:积分与导数互为逆运算
- 乘法法则: 链式法则:
- 洛必达法则:
5 thoughts
- 微积分的内容实际上不止这些,但是我认为这些用于计算机是够了,接下来去看《程序员数学》
- 需要记住的主要就是链式法则,涉及到反向传播的计算
Notes
- 微积分 calculus
- 举例:考虑圆的面积公式 将圆分解成圆环,圆环展开为矩形,平铺到数轴上方
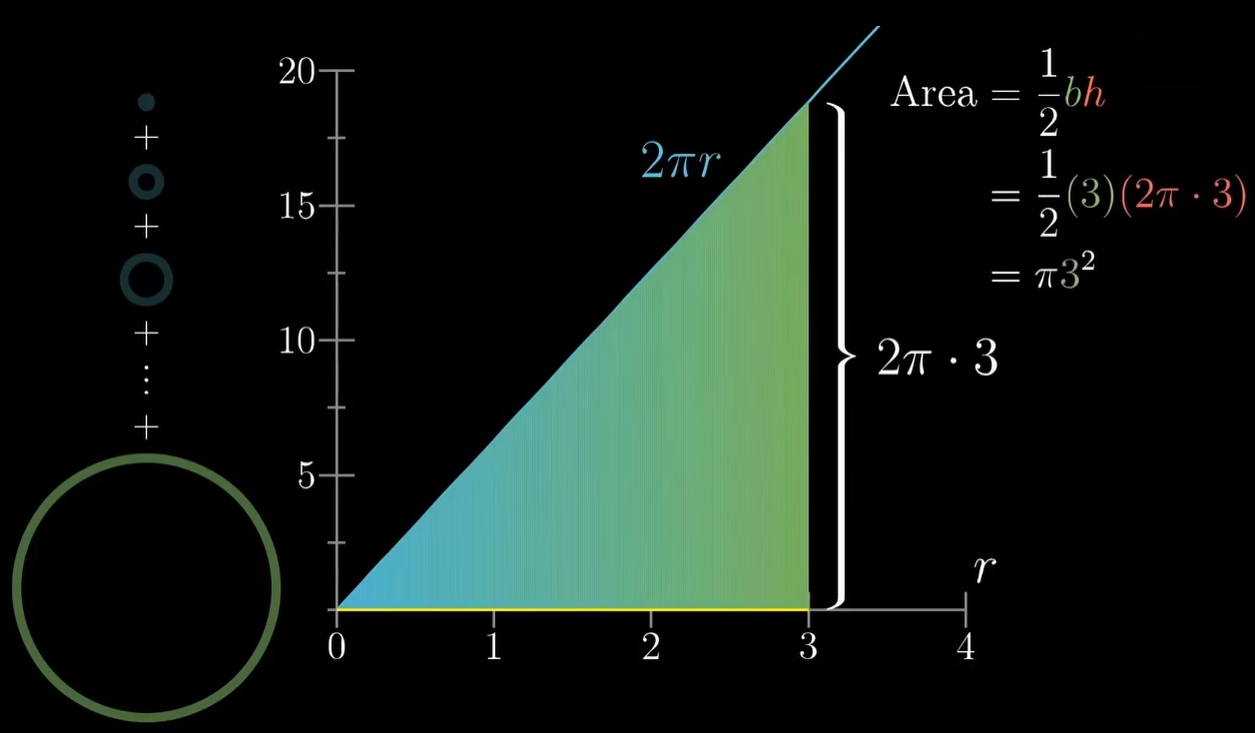
- 本质:许多实际问题能够分解相加,最后都是求解函数图像下面积
- 抽象化: 这就是导数
- 衡量函数对取值的微小变化有多敏感
- 举例:考虑圆的面积公式 将圆分解成圆环,圆环展开为矩形,平铺到数轴上方
- 微积分基本定理 ^16a500
- 积分与导数之间的来回转化——也就是某个图像下方面积函数的导数能够还原出定义这个图像的函数
- 积分与导数互为逆运算
- 导数 Derivatives
- 矛盾:瞬间的变化率没有意义,因为在一瞬间,运动是静止的
- 解决:只有在微小时间变化时,变化率(如速度)才有意义,因此微分 无限接近于 0
- 意义:经过图像上某一点切线的斜率,或某一点附近的变化率的近似
- 举例:
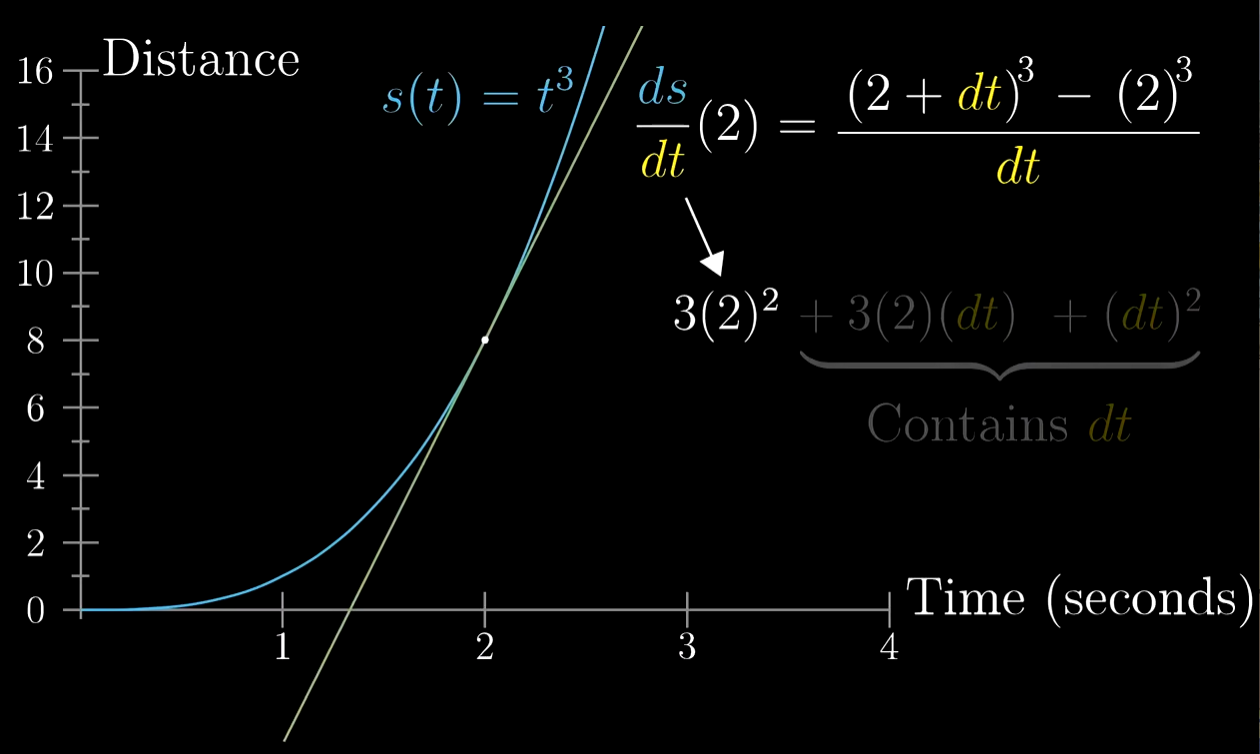
- 代入 后,当 逼近0,代数消去,得到一个定值
- 也就是说,
- 计算:
原理:高阶无穷小可以忽略
- 幂函数:
- 三角函数:
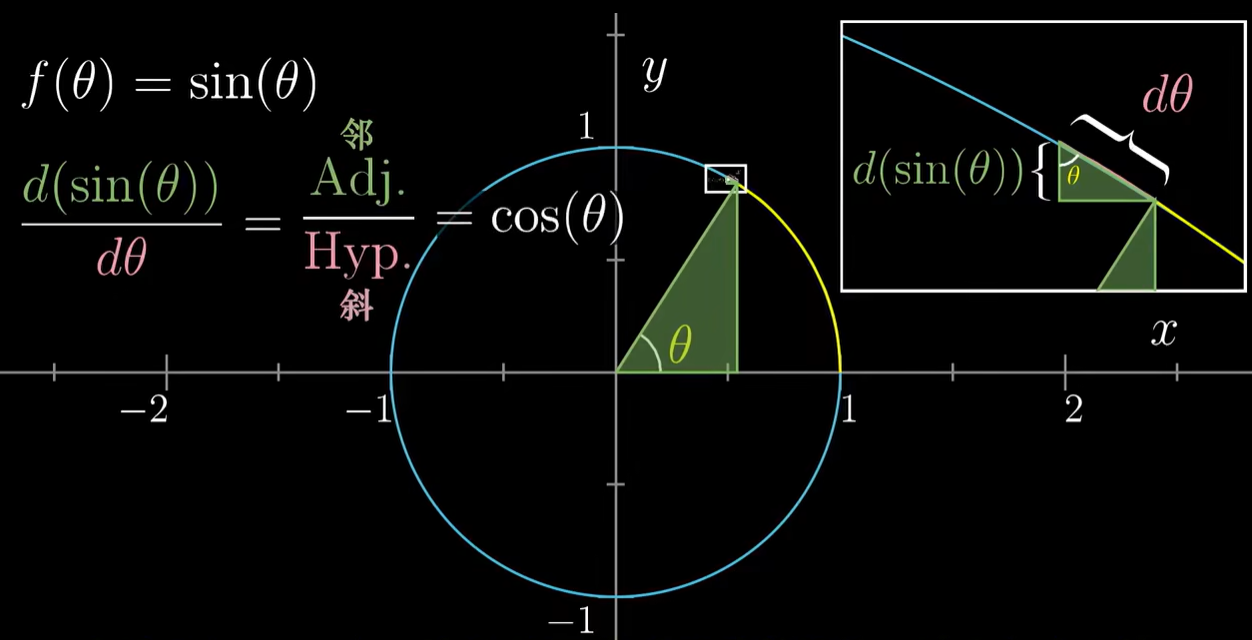 \frac{d(\sin(\theta))}{d\theta} = \cos(\theta)$$$$\frac{d(\cos(\theta))}{d\theta} = -\sin(\theta)
\frac{d(\sin(\theta))}{d\theta} = \cos(\theta)$$$$\frac{d(\cos(\theta))}{d\theta} = -\sin(\theta)
Info
所有组合方式:相加,相乘,复合
- 加法法则
- 乘积法则 左乘右导,右乘左导
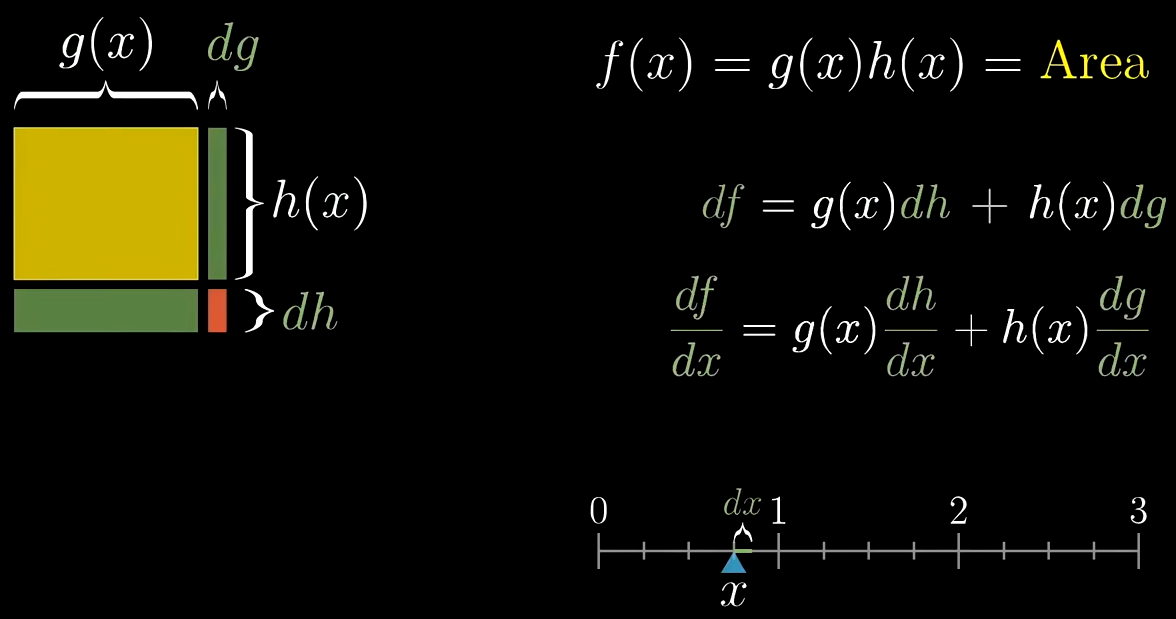
- 链式法则

- 指数函数的导数
- e的定义
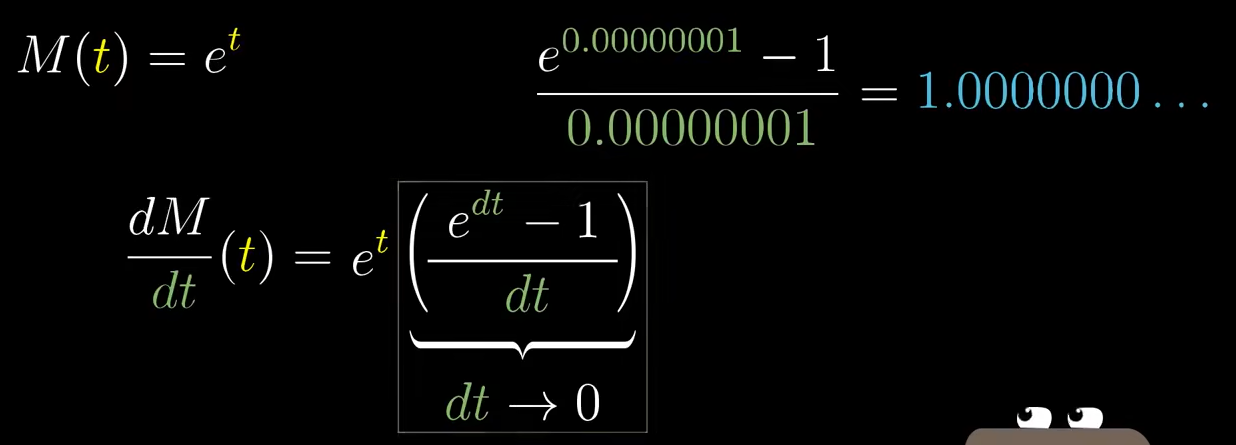 所有的指数函数都和它们的导数成比例,而对于e,该比例系数为1
所有的指数函数都和它们的导数成比例,而对于e,该比例系数为1 - 根据链式法则:
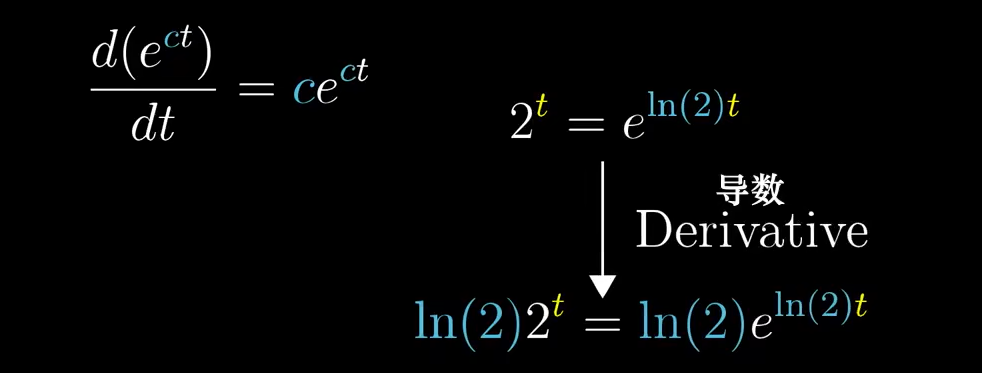
- 公式:
- e的定义
- 隐函数求导
- 方法:对等式两边分别求导
- 意义:
- 将等式移项到左侧,左侧可视作一个函数,右侧是一个常数
- 考虑从图像上移动微小的一步 ,因 无限小且右侧为常数,左侧函数变化率为0,则左侧函数导数为0
- 根据加法法则,对左侧求导后再进行移项,等同于等式两侧分别求导
- 举例:
- 极限
- 导数的正式定义:
- 极限的 定义
- 简单来说就是所求极限点附近长 、宽 的区间能否被缩小到极限点
- ~ 洛必达法则
- 适用:所求极限遇到分子分母均为0的情况,如
- 原理:
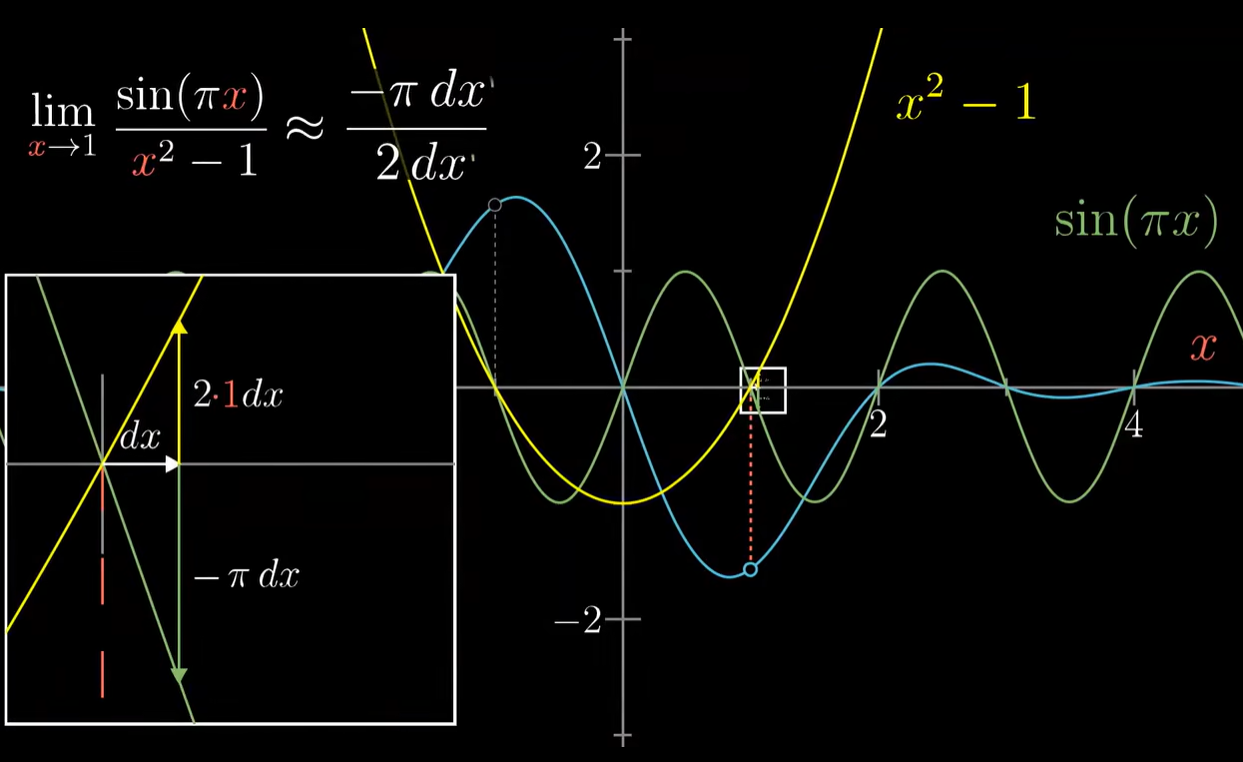
- 公式:
- 积分 Integral
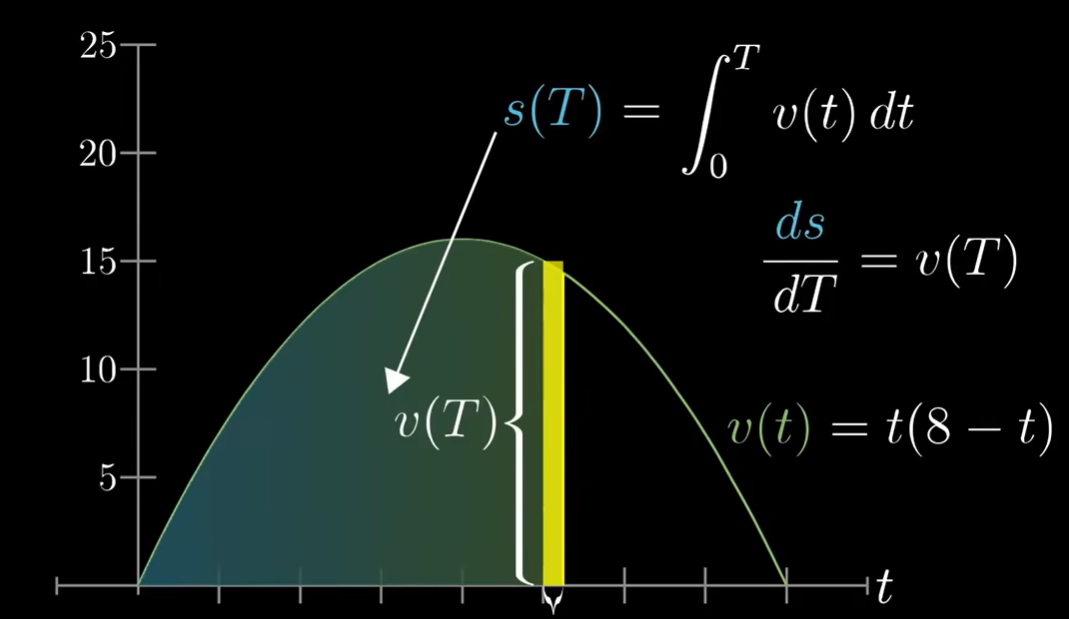
- 任一函数图像下方面积(该函数的积分)的导数等于原先的函数本身 例如距离与速度、时间的关系:
- 导数 ⇐> 原函数 Antiderivative
- 原函数实际上有无数个,因为常数的导数为0
- 微积分基本定理(具体)
- 求函数下面积
- 求连续函数某一区间的平均值
具有实际意义,比如说通过温度变化曲线图求半年内的平均气温
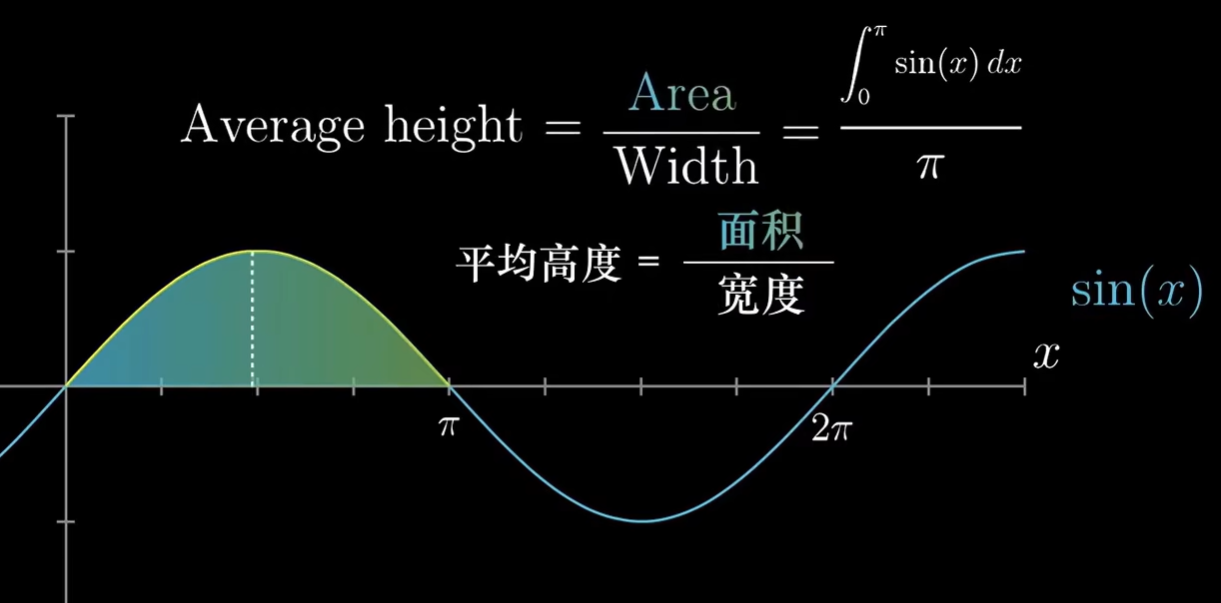 \begin{align}平均高度 & = 高度和/点的数量 \\ & = 高度和 / (区间宽度 / dx) \\ & = (高度和 \times dx) / 区间宽度 \end{align}公式右侧即原函数两点间斜率,即可以通过积分求得区间内平均切线斜率
\begin{align}平均高度 & = 高度和/点的数量 \\ & = 高度和 / (区间宽度 / dx) \\ & = (高度和 \times dx) / 区间宽度 \end{align}公式右侧即原函数两点间斜率,即可以通过积分求得区间内平均切线斜率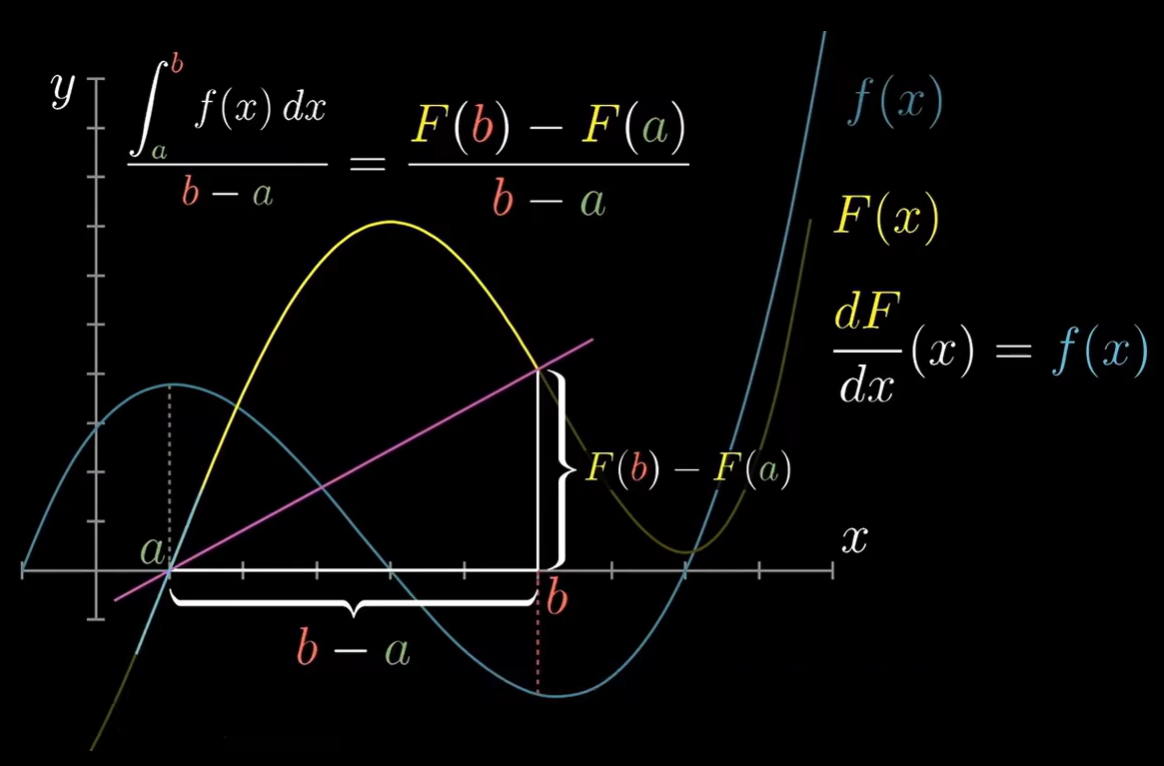
- 求函数下面积
- 微分方程