Diffusion Models

3 most important points

1. Diffusion Models 将扩散过程和逆扩散过程都建模为马尔科夫链，但经过推导，能够从初始跳跃至马尔科夫链上的任意时间步，无需逐步扩散，从而显著简化训练和采样计算
2. Diffusion Models 的模型是噪声预测器，DDPM 采用了一个 U-Net 结构的 Autoencoder
3. 通过重参数（引入一个随机变量）实现从高斯分布中采样这一步骤的梯度传播

5 thoughts

1. 超参数 $\beta$ 作为方差控制不同时间步的噪声强度，递增使得扩散初期图像保留主要语义结构，后期逐步向标准高斯收敛，保证整个分布平稳过渡
2. 均值受方差约束确定，是因为将图视为高维度信号，需要保证过程中能量守恒，信号不会被放大或缩小
3. 预测噪声而非均值能保持不同时间步上输出范围固定、梯度尺度一致，训练更稳定、收敛更快，且存在明确物理意义
4. 逆扩散过程中的方差由超参数直接定义，是因为方差只影响采样的多样性，对训练目标影响极小；如果预测方差，会增加梯度计算复杂度，且效果没有明显提升
5. 采样时添加噪声是为了保持生成过程随机性与多样性，否则只能生成单一样本

Notes

核心思想

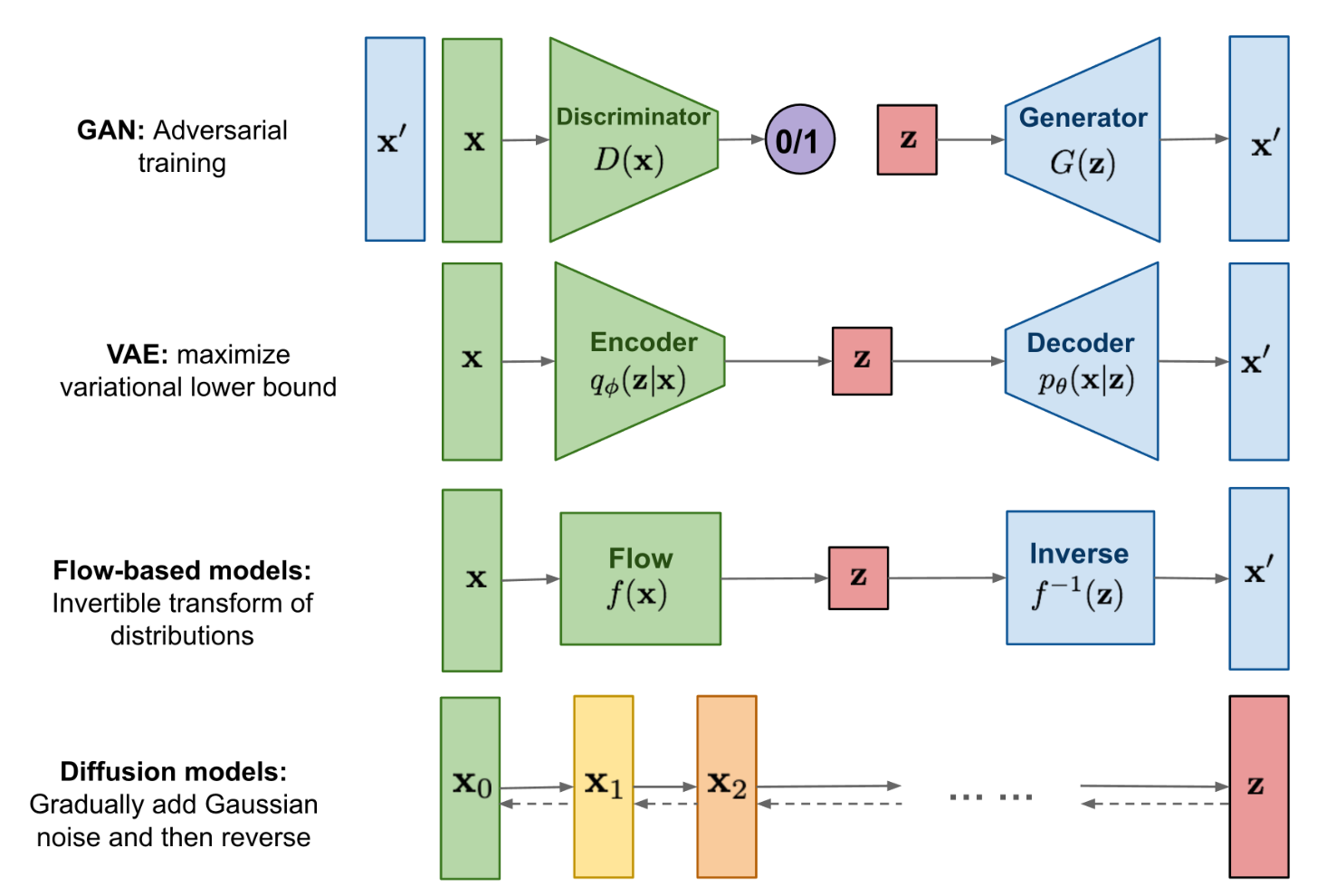
不同生成模型对比

• Diffusion models 和其他模型最大的区别是它的 latent code ($z$) 和原图是同尺寸大小的

• 设定：
  • 图像空间：所有图像组成概率分布 $\Theta$
  • 训练集：从 $\Theta$ 中一个分布 $p_{data}$ 中取出的随机样本 $x_0$
  • 模型：在 $\Theta$ 中与 $p_{data}$ 最接近的分布 $p_{\theta }$
• 原理：
  • 扩散（前向过程）：
    • 每个时间步，在 $x_{t-1}$ 上添加随机噪声，得到接近纯噪声的 $x_t$，使样本分布从 $p_{data}$ 逐渐逼近标准高斯分布 $\mathcal{N}(0,I)$
    • 该过程是一个马尔科夫链，由条件分布 $q(x_t|x_{t-1})$ 定义，表示基于前一状态的现状态的概率
    • 使用一系列的超参数 $\{{\beta }_t\in (0,1){\}}_{t=1}^T$ （ ${\beta }_t$ 随着 $t$ 增大而增大）来进一步定义条件分布，用以控制马尔科夫链上每一步的大小，它们表示高斯分布的方差
    • 最终： $q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathbf{I}),q(x_{1:T}|x_0)={\prod }_{t=1}^{T}q(x_t|x_{t-1})$
  • 逆扩散（逆向过程）：
    • 每个时间步，在从噪声分布 $\mathcal{N}(0,I)$ 中采样的 $x_t$ 上减去噪声生成 $x_{t-1}$，逐步逼近真实数据分布 $p_{data}$
    • 该过程也是一个马尔科夫链，由后验分布 $q(x_{t-1}|x_t)$ 定义，该概率分布未知，因此使用模型 $p_{\theta }(x_{t-1}|x_t)$ 来近似它
    • 未知情况下，使用 ${\mu }_{\theta }$ 近似均值，${\Sigma }_{\theta }$ 近似方差
    • 最终：$p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t)),p_{\theta }(X_{0:T})=p(x_T){\prod }_{t=1}^T{p}_{\theta }(x_{t-1}|x_t)$

为什么选择方差为超参数而不是均值？均值如何由方差取得？

• 直接定义方差 $\beta$ 可控制加噪强度
• 图像可看作高维信号，$\sqrt{1-{\beta }_t}$ 控制“保留多少旧能量”，${\beta }_t$ 控制“加入多少新噪声能量”；
• 上述定义可以保证整个过程每一步的总能量是恒定的，这样信号不会被放大或缩小，只是噪声比例在逐渐上升。

为什么 ${\beta }_t$ 是递增的？

• 如果 $\beta$ 恒定，早期图像可能被过快破坏，模型难以学习；后期噪声太弱则去噪训练信号不足。
• 所以 $\beta$ 通常递增（如线性或余弦调度），实现“先慢后快”的平滑加噪。
• 当 ${\beta }_t$ 递增且较小（如线性增长到 0.02 左右），最终方差稳定收敛到 1，不会发散或塌缩

技巧

Info

这个板块讲解如何简化原理中复杂、难以实现的部分

• 在马尔科夫链中跳步
  • 问题：
    • 在扩散过程中，逐步计算耗时耗算力
  • 解法：
    • 令 ${\alpha }_t=1-{\beta }_t$，并且 ${\bar{\alpha }}_t={\prod }_{i=1}^t{\alpha }_i$，利用独立高斯随机变量的和的性质和尺度变换性质，展开 $x_t$ 可以得到：\begin{align}x_t &= \sqrt{\alpha_t}x_{t-1} + \sqrt{1 - \alpha_t}\epsilon_{t-1} \quad \text{where } \epsilon_{t-1}, \epsilon_{t-2}, \cdots \sim \mathcal{N}(0, \mathbf{I})\\[6pt] &= \sqrt{\alpha_t\alpha_{t-1}}x_{t-2} + \sqrt{1 - \alpha_t\alpha_{t-1}}\bar{\epsilon}_{t-2} \quad \text{where } \bar{\epsilon}_{t-2} \text{ merges two Gaussians}\\[6pt] &= \cdots \\[6pt] &= \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}\end{align}
    • 因此任意时刻的 $x_t$ 满足： $q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)\mathbf{I})$
• 重参数（reparameterization trick）
  • 问题：
    • 从某个分布中随机采样一个样本的过程无法反向传播梯度，而在逆扩散过程中，需要从高斯分布 $z\sim \mathcal{N}(z;{\mu }_{\theta },{\sigma }_{\theta }^2\mathbf{I})$ 中采样 $x_t$
  • 解法：
    • 用独立随机变量 $ϵ$ 引导随机性，采样可以写成：$x_t={\mu }_{\theta }+{\sigma }_{\theta }\odot ϵ,ϵ\sim \mathcal{N}(0,\mathbf{I})$
    • 因为 ${\mu }_{\theta }$ 从模型中得到（${\sigma }_{\theta }$ 由超参数 ${\beta }_t$ 给定），所以整个采样过程仍然梯度可导

为什么逆扩散过程中的方差可以直接定义？

理论上 ${\Sigma }_{\theta }$ 是可学习的（比如 DDIM、Improved DDPM 都尝试学习它），因为真实的后验 $q(x_{t-1}|x_t)$ 的方差确实依赖于数据分布。

然而原始 DDPM 发现：即使把方差固定为常数（比如直接用 ${\beta }_t$），训练效果几乎不变。这是因为：

• 逆扩散的“随机性”主要由 ${ϵ}_{\theta }$ 决定；
• 方差只影响采样的多样性，对训练目标影响极小；
• 如果也去预测方差，梯度传播会更复杂，而且效果提升不明显。

• 均值的解析解
  • 问题：
    • 逆扩散过程中，均值 ${\mu }_{\theta }$ 如何从模型中得到？
  • 解法：
    • 在知道 $x_0$ 的情况下，考虑后验分布构成的 $q(x_{t-1}|x_t,x_0)$
    • 根据乘法定理和贝叶斯公式展开：\begin{align*}q(x_{t-1}|x_t, x_0) &= \frac{q(x_t, x_0, x_{t-1})}{q(x_t, x_0)} \\[6pt] &= \frac{q(x_0)q(x_{t-1}|x_0)q(x_t|x_{t-1}, x_0)}{q(x_0)q(x_t|x_0)} \\[6pt]&= q(x_t | x_{t-1}, x_0) \cdot \frac{q(x_{t-1} | x_0)}{q(x_t | x_0)}\end{align*}
    • 由于 $x_t$ 与 $x_0$ 无关，所以都是已知的，根据高斯分布的概率密度函数展开，合并指数部分：$\exp \left(-\frac{1}{2}\left(\frac{(x_t-\sqrt{{\alpha }_t}{x}_{t-1}{)}^2}{{\beta }_t}+\frac{(x_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{x}_0{)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^2}{1-{\bar{\alpha }}_t}\right)\right)$
    • 整理为与 $x_{t-1}$ 相关的：$\exp \left(-\frac{1}{2}\left(\underset{x_{t-1}\text{方差}}{\underbrace{\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)x_{t-1}^2}}-\underset{x_{t-1}\text{均值}}{\underbrace{\left(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0\right)x_{t-1}}}+\underset{\text{与}{x}_{t-1}\text{无关}}{\underbrace{C(x_t,x_0)}}\right)\right)$
    • 同时，后验分布可以直接写成：\begin{align} q (x_{t-1}|x_t, x_0) = \mathcal{N}(x_{t-1}; \tilde{\mu}(x_t, x_0), \tilde{\beta}_t \mathbf{I}) &\propto \exp\left( -\frac{(x - \tilde{\mu})^2}{2\tilde{\beta}_t^2} \right)\\ &=\exp\left( -\frac{1}{2} \left( \frac{1}{\tilde{\beta}_t^2} x^2 - \frac{2\tilde{\mu}}{\tilde{\beta}_t^2} x + \frac{\tilde{\mu}^2}{\tilde{\beta}_t^2} \right) \right)\end{align}
    • 解方程组，把 $x_0$ 和 $x_{t-1}$ 都用 $x_t$ 表示，代入得：${\tilde{\mu }}_t=\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\epsilon }_t\right),{\tilde{\beta }}_t=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t$
    • 这样，就可以用模型 ${ϵ}_{\theta }(x_t,t)$ 预测当前步噪声 ${\epsilon }_t$，再代入公式得到 ${\tilde{\mu }}_t$

为什么不直接预测均值？

如果直接预测 ${\mu }_{\theta }(x_t,t)$，不同 $t$ 的梯度尺度会严重不均：

• 早期（$t$ 小）时 $x_t$ 仍接近 $x_0$，误差小
• 后期（$t$ 大）时 $x_t$ 几乎是纯噪声，预测难度高，梯度极不稳定

预测噪声 ${ϵ}_{\theta }$ 后：

• 所有时间步都来自相同分布 $\mathcal{N}(0,I)$
• 模型输出范围固定，梯度尺度一致
• 可统一训练目标为简单的 L2 loss

同时：

• ${ϵ}_{\theta }$ 预测有明确的物理意义（“识别图片中的噪声”），符合直觉
• 使模型能自然处理不同噪声强度（不同 $t$）的输入，泛化更强

训练

Warning

由于完整的损失函数推导过于复杂，这里略过大部分过程

• 优化目标
  • 使用极大似然估计求模型参数，即最大化模型预测分布的对数似然
  • 从 Loss 下降的角度就是最小化负对数似然
  • 与 VAE 类似，使用变分下界（VLB）也就是证据下界（ELBO）来优化负对数似然

关于 VLB

变分下界（Variational Lower Bound, VLB），也称为证据下界（ELBO），是用于近似优化难以直接计算的对数似然（如生成模型中的边缘似然 $\log p(x)$）的一种方法。通过引入一个可学习的近似后验分布 $q(z|x)$，VLB 将负对数似然分解为一个可计算的下界和一个非负的 KL 散度项：

$$\log p(x)\ge {\mathbb{E}}_{q(z|x)}[\log p(x|z)]-\mathrm{KL}(q(z|x)\Vert p(z))=\text{ELBO}.$$

最大化 VLB 等价于最小化负对数似然的上界，从而间接提升模型对数据的拟合能力。

其中的 KL 散度项衡量两个分布之间的距离，为 0 的时候两个分布一致；所以这里是在拉近模型分布和后验分布的距离。

• 模型
  • 不是直接预测 $\tilde{\mu }(x_t,x_0)$，而是用模型 ${ϵ}_{\theta }(x_t,t)$ 预测当前步噪声 ${\epsilon }_t$，再代入公式得到 ${\tilde{\mu }}_t$
  • DDPM 采用了一个 U-Net 结构的 Autoencoder 作为 ${ϵ}_{\theta }$
• 算法
  1. 采样
     • 在训练集中采样 $x_0$
     • 在常数 $\{1,\cdots ,T\}$ 中采样一个 $t$
     • 在高斯分布 $N(0,I)$ 中采样一个与图像大小相同的噪声 $ϵ$
  2. 梯度下降，训练 ${ϵ}_{\theta }(x_t,t)$ ：$Loss=||ϵ-{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ,t)|{|}^2$
  • 直觉理解：将真实图片 $x_0$ 和噪声 $ϵ$ 以一定比例混合在一起输入，同时输入混合比例 $t$，训练噪声预测器使得它的输出接近从高斯分布中采样出的 $ϵ$（能够认出混合在图片中的噪音）

采样

1. 在高斯分布 $N(0,I)$ 中采样一个与图像大小相同的噪声 $x_T$
2. 当 $t=T,...,1$：
   • 在高斯分布 $N(0,I)$ 中采样一个与图像大小相同的噪声 $z$；在 $t=1$ 时取 $z=0$
   • 计算下一循环输入 $x_{t-1}=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))+{\sigma }_{t}z$
3. 返回 $x_0$

• 直觉理解：就是先识别 $x_T$ 中的噪声，将它不断以一个比例从 $x_T$ 中去除，乘一个常数，再加上一个噪声

采样过程为何又加噪声？

• 加上随机噪声 $z\sim N(0,I)$ 是为了保持采样多样性
• 逆扩散的每一步是随机采样而不是确定性去噪；如果不加 $z$，生成过程会退化为单一样本，不再具有“生成模型”性质

扩展

Todo

以下是很久以前的笔记，需要更新

Stable Diffusion

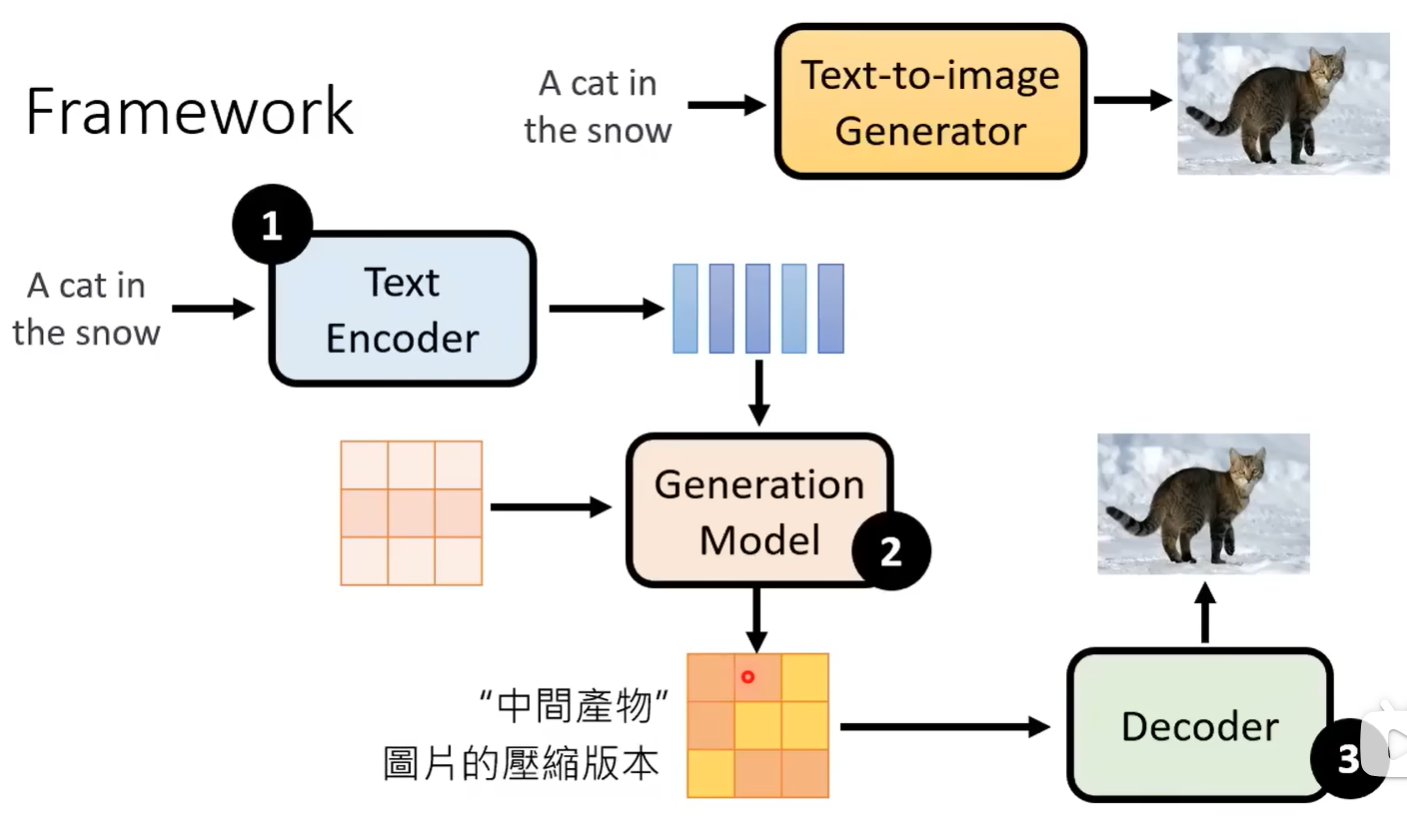
1. Text Encoder
   • 把文字描述转化为矩阵
2. Generation Model
   • 一般用 diffusion model，左侧那个矩阵应该是给定噪声
3. Decoder
   • 类 AE 的 decoder

VQ-Diffusion

论文名称：Vector Quantized Diffusion Model for Text-to-Image Synthesis 发表时间：2022.3.3 论文链接：https://arxiv.org/abs/2111.14822 论文代码：https://github.com/microsoft/VQ-Diffusion

• 动机：
  • 分辨率过高的图像不利于 transformer 建模
• 结构：
  1. 使用 VQ-VAE 将图像压缩到离散的 codebook 空间
  2. 在 codebook 中 diffusion：引入 mask & replace
     • 加噪声：随机 mask 一个 code 或者 replace 成另外一个 code，这样就能把原 code 变成一个随机噪声向量
     • 形成概率转移矩阵 $Q_t$，有 $q(x_t|x_{t-1}):=Q_t{x}_{t-1}$
       • ${\alpha }_t$：code 保持原样的概率
       • ${\beta }_t$：replace 的概率
       • ${\gamma }_t$：mask 的概率
  3. 利用 transformer 网络把 code 噪声和文本信息 decode 成原本的 code
  4. 经由 decoder 恢复到原本的空间中
• 指标：
  1. FID：把真实图像和生成图像输入到训练好的 CNN 分类器中，如果两组的 representation 越接近，效果就越好；假设 representation 都是高斯分布，得到他们之间的 FID 也就是 frechet distance。这个指标越小越好。但是需要采样大量样本（例如 10K）来进行评估。（真实性评估）
  2. CLIP：Contrastive Language-Image Pre-Training，由 text encoder 和 image encoder 组成。训练好这个模型，把图像和与其对应的文字输入进去，编码出来的向量越近越好。（文本相近性评估）

Related

• 马尔科夫链
• 概率论

Reference

• Diffusion Models：生成扩散模型
• 由浅入深了解Diffusion Model