位姿

3 most important points

1. 位姿就是位置+姿态
2. 姿态的表示：旋转矩阵、欧拉角、轴角和四元数
3. 位姿有多种含义，包括物品之间、坐标轴之间和物品相对坐标轴

5 thoughts

1. 四元数最常用

Notes

概览

什么是位姿

顾名思义，位姿就是位置+姿态。

问：假设一个人在一座大楼里，如何描述这个人当前的状态？ 答：大楼的经度（x）、纬度（y）和海拔高度（z），以及这个人当前的姿态（躺平/站立/侧卧）

• 定义
  • 参考坐标系：$A$
  • 以物体为原点的坐标系：$P$
  • 惯例使用右手坐标系
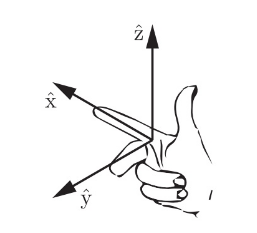
• 位置的表示
  • 位置矢量：${}^{A}P=\left[\begin{array}{c}{}^{x}p\\ {}^{y}p\\ {}^{z}p\end{array}\right]={\left[\begin{array}{ccc}{}^{x}p,& {}^{y}p,& {}^{z}p\end{array}\right]}^T$

姿态的表示

姿态	轴	参数	公式	特点
[[#旋转矩阵	旋转矩阵]]	固定坐标系	9	${}_P^{A}R=[{{}^{A}x}_P{{}^{A}y}_P{{}^{A}z}_P]$
欧拉角	固定坐标系	3	$R_{XYZ}(\gamma ,\beta ,\alpha )=R_Z(\alpha )R_Y(\beta )R_X(\gamma )$	有 12 种旋转顺序
欧拉角	自身坐标系	3	$R_{Z^{\prime }{Y}^{\prime }{X}^{\prime }}(\alpha ,\beta ,\gamma )=R_Z(\alpha )R_Y(\beta )R_X(\gamma )$	有 12 种旋转顺序
[[#轴角	轴角]]	任意矢量	4	${}_B^{A}R(A^K,\theta )$
四元数	任意矢量	4	$q=w+x\times i+y\times j+z\times k$ $p^{\prime }=qp{q}^{-1}$	可以避免欧拉角带来的困难与歧义

• 位姿描述的多个含义
  1. 表示特定参考坐标系下某个物体（点）的位置和姿态，比如我们描述参考坐标系 $A$ 中物体（点）$P$ 的位置和姿态
  2. 表示两个坐标系之间的位姿关系，比如位置可以表示坐标系 $A$ 和坐标系 $B$ 原点位置关系，姿态可以表示两个坐标系坐标轴的朝向关系 $B={\{}_B^{A}R{,}^A{P}_{Bo}\}$
  3. 如果把坐标系固定在物体上，可以表示两个物体之间的位姿关系，比如自行车前轮和后轮之间的关系

旋转矩阵

旋转矩阵，即 $P$ 的三个轴相对于参考坐标系 $A$ 三个轴的共 9 个角度的余弦值组成的 $3\times 3$ 矩阵

$${}_P^{A}R=[{{}^{A}x}_P{{}^{A}y}_P{{}^{A}z}_P]=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$

两个向量的点乘为两个向量的长度与它们夹角余弦的积，所以 $r_{11}$ 可以表示为单位向量 $P_x$ 与 $A_x$ 的点积，旋转矩阵就可以写为下面的形式

$${}_P^{A}R=\left[\begin{array}{ccc}{P}_x\cdot A_x& P_y\cdot A_x& P_z\cdot A_x\\ P_x\cdot A_y& P_y\cdot A_y& P_z\cdot A_y\\ P_x\cdot A_z& P_y\cdot A_z& P_z\cdot A_z\end{array}\right]$$

该旋转矩阵描述了从坐标系 $P$ 到坐标系 $A$ 的旋转

将 ${}_P^{A}R$ 进行转置可得 ${}_P^A{R}^T$

$${}_P^A{R}^T=\left[\begin{array}{ccc}{P}_x\cdot A_x& P_x\cdot A_y& P_x\cdot A_z\\ P_y\cdot A_x& P_y\cdot A_y& P_y\cdot A_z\\ P_z\cdot A_x& P_z\cdot A_y& P_z\cdot A_z\end{array}\right]$$

可以看出 ${}_P^A{R}^T$ 其实表示坐标系 $P$ 作为参考坐标系下坐标系 $A$ 的姿态，即：

该矩阵描述了从坐标系 $A$ 到坐标系 $P$ 的旋转

则有：

$${}_P^A{R}^T{=}_A^{P}R{=}_P^A{R}^{-1}$$

矩阵的逆等于矩阵的转置，这说明旋转矩阵是正交矩阵

固定轴欧拉角

将坐标系 $A$ 围绕坐标系 $A$ 的轴进行旋转得到坐标系 $B$ ，称为固定轴欧拉角。欧拉角由 3 个角度构成。

可视为对向量旋转；将旋转进行拆分，按 xyz 的旋转顺序，代入旋转矩阵得：

$$R_{XYZ}(\gamma ,\beta ,\alpha )=R_Z(\alpha )R_Y(\beta )R_X(\gamma )=\left[\begin{array}{ccc}c\alpha c\beta & c\alpha s\beta s\gamma -s\alpha c\gamma & c\alpha s\beta c\gamma +s\alpha s\gamma \\ s\alpha c\beta & s\alpha s\beta s\gamma +c\alpha c\gamma & s\alpha s\beta c\gamma -c\alpha s\gamma \\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{array}\right]$$

其中 $c$ 代表 $cos$，$s$ 代表 $sin$

除 xyz，还有多种旋转顺序：

• xyz, xyx, xzy
• xzx, yzx, yzy
• yxz, yxy , zxy
• zxz, zyx, zyz

非固定轴欧拉角

将坐标系 $A$ 围绕自身坐标轴旋转得到坐标系 $B$ ，称为非固定轴欧拉角。

从 $B$ 到 $A$ 的旋转矩阵如下所示：

$$\frac{A}{B^{\prime }}R\cdot P_Z=P_0$$ $$\frac{B^{\prime }}{B^{\prime \prime }}R\cdot P_{ZY}=P_Z$$ $$\frac{B^{\prime \prime }}{B}R\cdot P_1=P_{ZY}$$ $$\frac{A}{B^{\prime }}R\cdot \frac{B^{\prime }}{B^{\prime \prime }}R\cdot \frac{B^{\prime \prime }}{B}R\cdot P_1=P_0$$

则：

$$R_{Z^{\prime }{Y}^{\prime }{X}^{\prime }}(\alpha ,\beta ,\gamma )=R_Z(\alpha )R_Y(\beta )R_X(\gamma )=\left[\begin{array}{ccc}c\alpha c\beta & c\alpha s\beta s\gamma -s\alpha c\gamma & c\alpha s\beta c\gamma +s\alpha s\gamma \\ s\alpha c\beta & -s\alpha s\beta s\gamma +c\alpha c\gamma & -s\alpha s\beta c\gamma -c\alpha s\gamma \\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{array}\right]$$

轴角

将坐标系 $A$ 围绕 $A$ 内任意矢量 ${}^{A}K$ 按右手定则旋转 $\theta$ 角度得到坐标系 $B$，称为轴角。

${}^{A}K$ 是单位矢量，${}^{A}K=[k_x,k_y,k_z{]}^T$

旋转之后坐标系 $B$ 在坐标系 $A$ 下的姿态可以用旋转矩阵 ${}_B^{A}R(A^K,\theta )$ 表示。

两个坐标系之间的任何姿态都可以通过绕一个矢量旋转特定的角度得到。

四元数

3 most important points

1. 四元数空间的基向量是 $[1,i,j,k]$，虚数能丝滑表示旋转
2. 四元数可以避免欧拉角带来的困难与歧义（比如 $0°$ 与 $360°$）
3. 通过四元数乘法 $qp{q}^{-1}$ 即可计算点 $p$ 旋转后的位置，$q=w+x\times i+y\times j+z\times k$

Link to original

四元数转旋转矩阵：

$$R=\left[\begin{array}{ccc}1-2y^2-2z^2& 2(xy-zw)& 2(xz+yw)\\ 2(xy+zw)& 1-2x^2-2z^2& 2(yz-xw)\\ 2(xz-yw)& 2(yz+xw)& 1-2x^2-2y^2\end{array}\right]$$

旋转矩阵转四元数：

$$x=\frac{r_{32}-r_{23}}{4w}$$ $$y=\frac{r_{13}-r_{31}}{4w}$$ $$z=\frac{r_{21}-r_{12}}{4w}$$ $$w=\frac{1}{2}\sqrt{1+r_{11}+r_{22}+r_{33}}$$

轴角转四元数：

$$x=k_x\sin (\theta /2)$$ $$y=k_y\sin (\theta /2)$$ $$z=k_z\sin (\theta /2)$$ $$w=\cos (\theta /2)$$

Related

Reference

• 姿态的多种表示