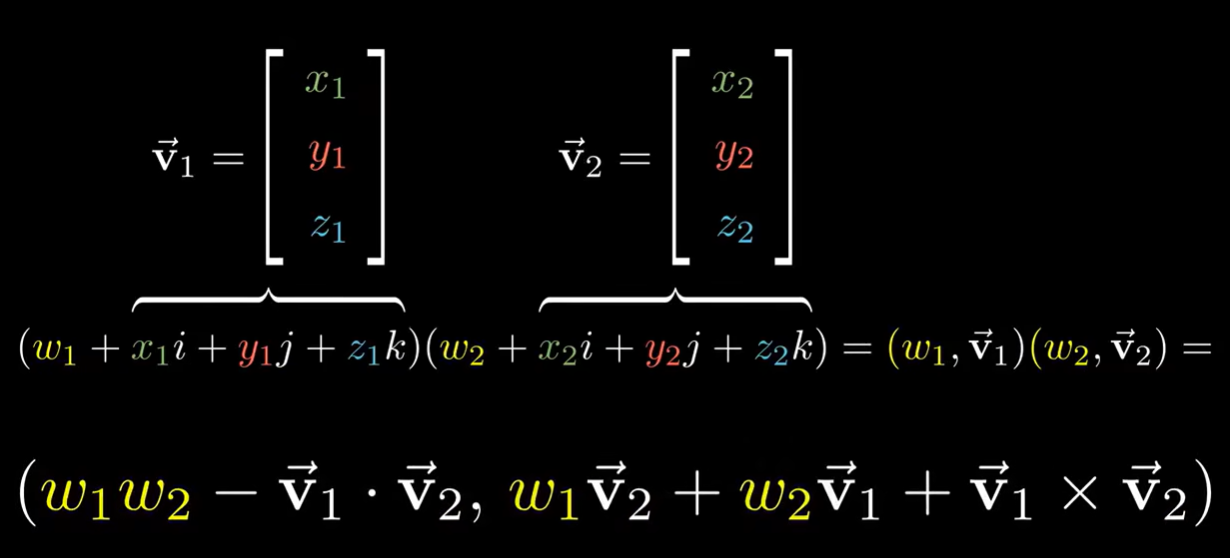3 most important points
- 四元数空间的基向量是 ,虚数能丝滑表示旋转
- 四元数可以避免欧拉角带来的困难与歧义(比如 与 )
- 通过四元数乘法 即可计算点 旋转后的位置,
5 thoughts
- 欧拉角描述旋转结果,而四元数描述旋转过程
- “三明治”乘法是为了消除拉伸虚数轴带来的空间扭曲
Notes
四元数的四个数字由一个实部和三个虚部组成,是一个超复数形式:
四元数能够很好地表示四维旋转。
从复平面开始,以实数为 轴,虚数为 轴,将平面上任意向量乘以 表示逆时针旋转 。
从基向量来看整个空间的变化,,即:
而 ,即:
这是一个逆时针旋转 的线性变换:
增加一个虚数轴,使 为基向量,就可以类似地描述三维空间中的旋转;而再增加一个虚数轴,使 为基向量,就是四元数。
四元数与向量
注意到,向量其实是实部为 0 的四元数 向量叉乘是四元数乘法的一部分:
等式右侧就是三阶行列式公式
用叉乘描述四元数乘法:
四维旋转如何映射到三维空间呢?这就需要用到球极投影(Stereographic projection)
以 空间为例,从点 出发,与单位球每个点的连线过 平面的点,就是该单位球在 平面上的球极投影。

由此,四维球体被投影到 三维空间;当四维球体沿 平面旋转时,可视作 轴上 的循环,每个节点代表逆时针旋转 。
同时, 空间的三维球体(与 轴垂直)也在随四维球体旋转而旋转,它在 平面的投影平面随之转动,如下图所示:
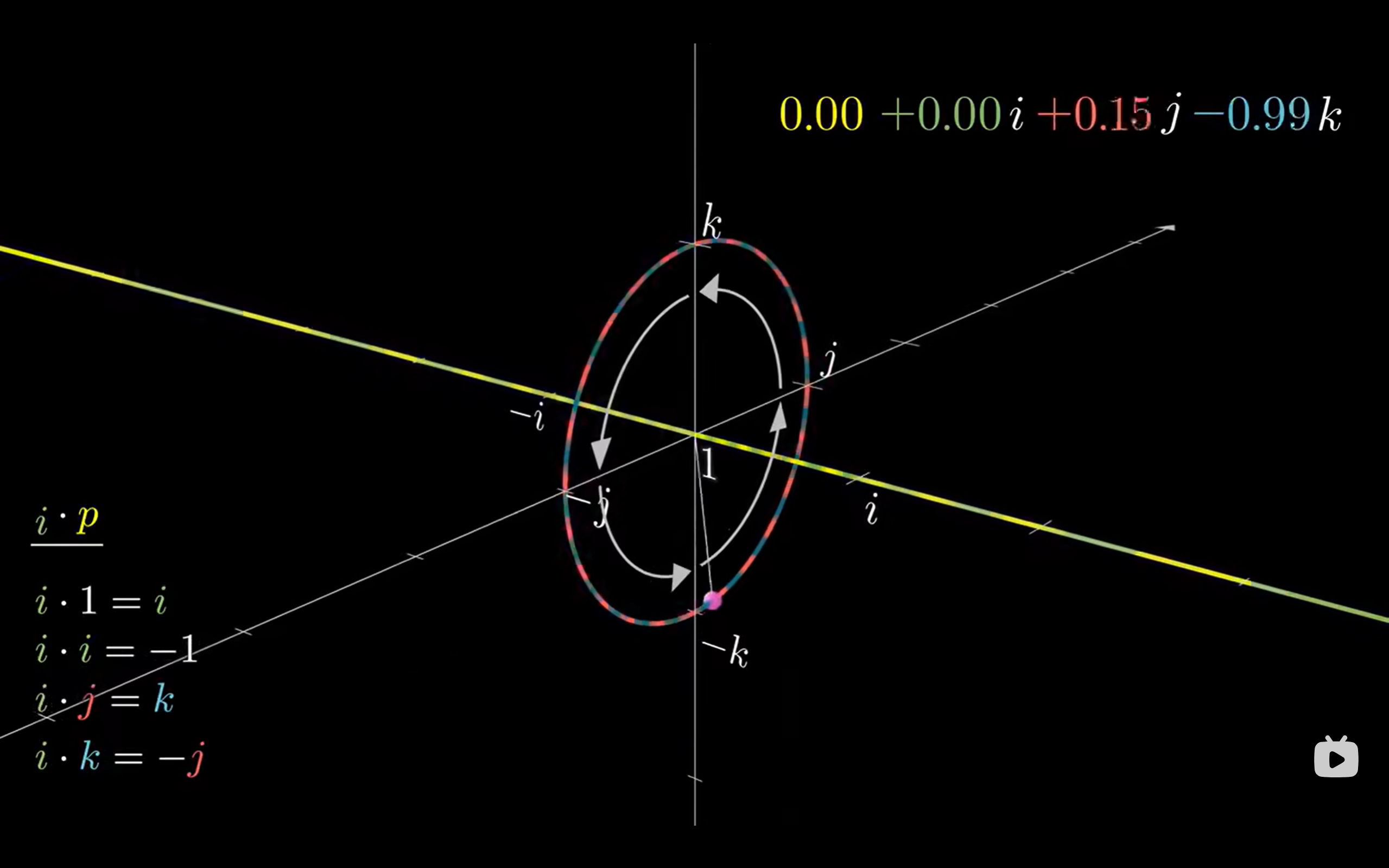
对空间的任何变换都可以通过对基向量进行线性变换来表示,也可以用四元数乘法来表示空间旋转。
假设在 空间中有向量 和 :
分数部分表示 起到的旋转作用,括号部分表示 对 起到的放缩作用。
左乘时, 对 的旋转作用遵循右手螺旋定则;右乘时,遵循左手螺旋定则。 上图中为右手螺旋定则,即大拇指为 轴朝向, 平面的转动方向为四指朝向
为什么使用四元数来描述三维旋转?
通常,欧拉角可以正确表示物体姿态,但当任意两条旋转轴重合时,系统就会失去一个自由度;在两个不同方向上插值时,也会造成困难和歧义。
而四元数可以完全避免上述问题: 四元数比三维多一个维度,且在三维投影空间中的一个点同时对应四维空间中的两个点,解决了旋转过程中 与 带来的纷争。
可以说: 欧拉角描述旋转结果,而四元数描述旋转过程。
通过这一公式就可以轻松计算某个点经过某个角度旋转后的位置:

记旋转轴对应的实部为 0 的单位向量为 ,则:
采用“三明治”乘法的原因是需要保持在 空间中三维球体的形态。
以 轴为例,当改变 中 的参数 时, 轴的单位向量实际上在被拉伸——从 到无穷远(-1),但是此时 仅按照右手定则顺时针旋转,尺度不改变。这会导致整个三维空间的形变;而为了取消这一形变,在 的 的恰好是 的 的负数。
了解“三明治”的作用后,理解这个式子就简单了:
左乘是按右手定则旋转,右乘是按左手定则旋转,相当于在取消形变的同时,按照相同方向各旋转一半的目标角度。
当然,也可以先沿 转 ,再沿 转 ,也就是:
二者等价,展开后各参数一致。