3 most important points
- 一对基向量可以表示一个空间,而空间可以用不同的基向量来表示
- 矩阵表示线性变换,实际上是一种函数,描述空间的运动,或者说基向量的运动;当矩阵不是方阵的时候,对应变换使空间发生升维或者降维
- 通过奇异值分解(SVD),任何矩阵 A=UΣV⊤,分解为旋转、维度缩放、再次旋转三个步骤
5 thoughts
- 矩阵的行列式即线性变换对面积(体积)产生改变的比例(有向)
- 通过基变换 A−1MA,将 M 转换为另一种空间表达下的对角矩阵,即可简便进行矩阵的幂运算
- 特征向量是在线性变换中仅被拉伸或压缩,而没有离开原本所在直线的向量;特征值是衡量特征向量在变换中拉伸或压缩比例的因子
- 关注特征向量,我们可以具象化某种线性变换,比如以特征向量为轴进行旋转
- 通过基变换使特征向量作为基向量,便于计算
Notes
- 计算机学科中的定义
- 运算
- 基向量 basis vectors
- i^ 为x轴长度为1的向量,j^ 为y轴长度为1的向量
- 从数字列表的角度出发,把向量中的每个数字视作标量scalar,该向量就是这些标量缩放基向量得到的结果
- 张成的空间 span
- 给定任意两个二维向量,其 span 就是二者所有的线性组合 linear combinations av+bw
- 两个三维向量的线性组合构成 flat sheet 平面,三个构成三维空间
不考虑共线或者共面的情况
- 线性相关 Linearly dependent
- 有多个向量,可以移除其中一个而不减少 span
例如共线的两个向量是线性相关的
- 或者说,这个向量可以表示为其它向量的线性组合
比如说,三维空间中的第三个向量落在另两个构成的 flat sheet 中
- 线性无关 Linearly independent
- 空间的基 The basis of a vector space
- @ 线性变换 Linear transformation
- 定义:transformation = function,实际上是一种函数 应用一个矩阵进行线性变换,相当于应用了一个函数
- 可视化:一种运动,输入向量到输出向量——所有向量视为点时,就是空间的运动
- 线性:网格线保持平行且等距分布 直线必须是直线,原点必须在原点
- Grid lines remain parallel and evenly spaced.
- 描述:基向量的变换
- 基础操作:
- 矩阵 Matrix
- 矩阵向量乘法:缩放基向量再相加
- 基向量的组合
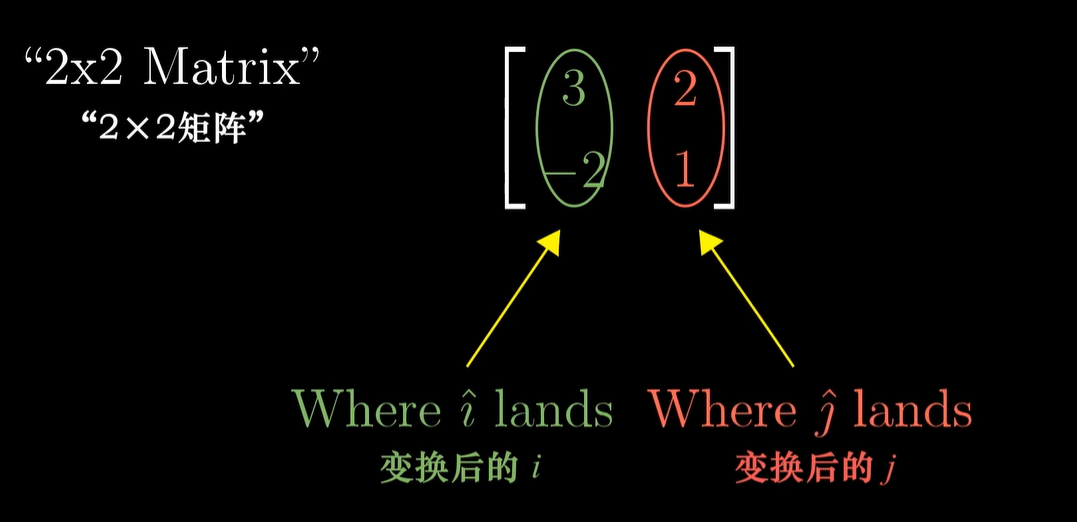
- 根据基向量的线性组合得到结果
 对于单一矩阵乘以向量,左乘变换行,右乘变换列
对于单一矩阵乘以向量,左乘变换行,右乘变换列
- 矩阵乘法:基向量的多次变换
- 复合矩阵是最初两个矩阵的积 the product of the original two matrices
 将两个函数复合时,需要从右向左读 —— f(g(x)),矩阵也一样
将两个函数复合时,需要从右向左读 —— f(g(x)),矩阵也一样
- Associativity 结合律
- 矩阵的逆 Inverse
- invertible / non-singular 可逆/非奇异矩阵
基向量 ⇒ 线性变换 ⇒ 可逆矩阵 ⇒ 线性变换(逆) ⇒ 基向量
可以想象一组向量必须能通过线性变换得到基向量,那么它们肯定是线性无关的
- 奇异矩阵 singular
- ~ 行列式 determinant
- 直观定义:线性变换对面积(体积)产生改变的比例 这就是对整个空间产生的影响
- 负数:变换的过程中反转了空间取向 invert the orientation of the space
- 三阶行列式计算公式
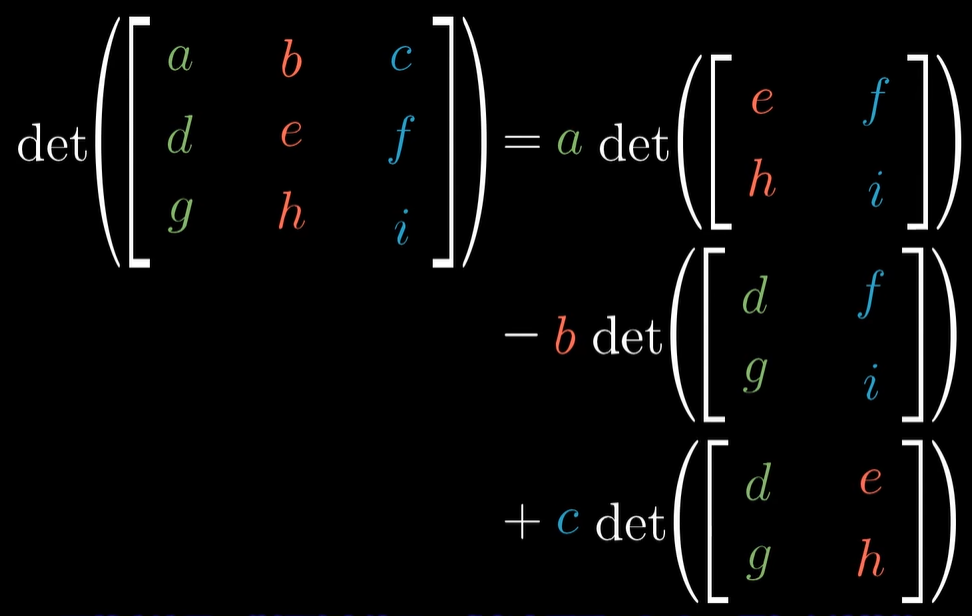
- 两个矩阵乘积的行列式 = 两个矩阵行列式乘积
视作两次变换,第一次比例变换和第二次比例变换的乘积就是总比例的变换
- 列空间 column space
- 所有可能的输出向量构成的集合 列(变换后的基向量)张成的空间
- 秩 rank
- 列空间的维数 线性变换后空间的维数
- 满秩:列空间的维数与输入空间的维数相等
- 零空间/核 null space/kernel
- 点积 dot product
- 计算:
- 两个维数相同的向量,各维度分别相乘后相加
- v在w上的投影长度乘以w的长度
- 当向量同向时为正,垂直时为0,异向时为负
- 几何意义:
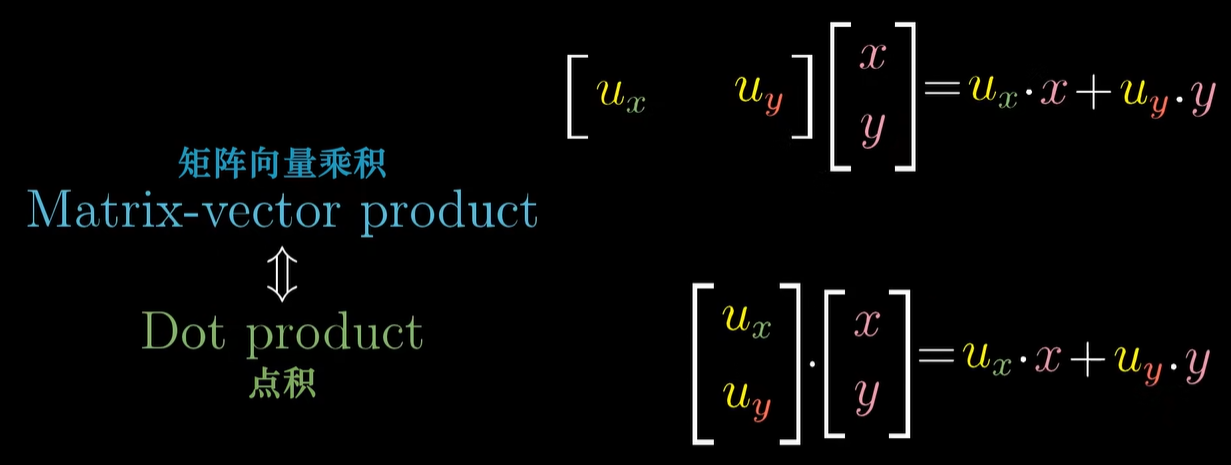 将一个二维向量投影到一个一维空间,这个变换用 1×2 矩阵来描述,且该一维空间就是该矩阵转置得到的向量所在的数轴
因此,可以通过投影长度相乘来计算点积
将一个二维向量投影到一个一维空间,这个变换用 1×2 矩阵来描述,且该一维空间就是该矩阵转置得到的向量所在的数轴
因此,可以通过投影长度相乘来计算点积
- 叉积 cross product
- 计算:
- 两个向量v和w组成的平行四边形的面积;v在w右侧的时候,v乘w为正,否则为负
- 计算行列式获得值
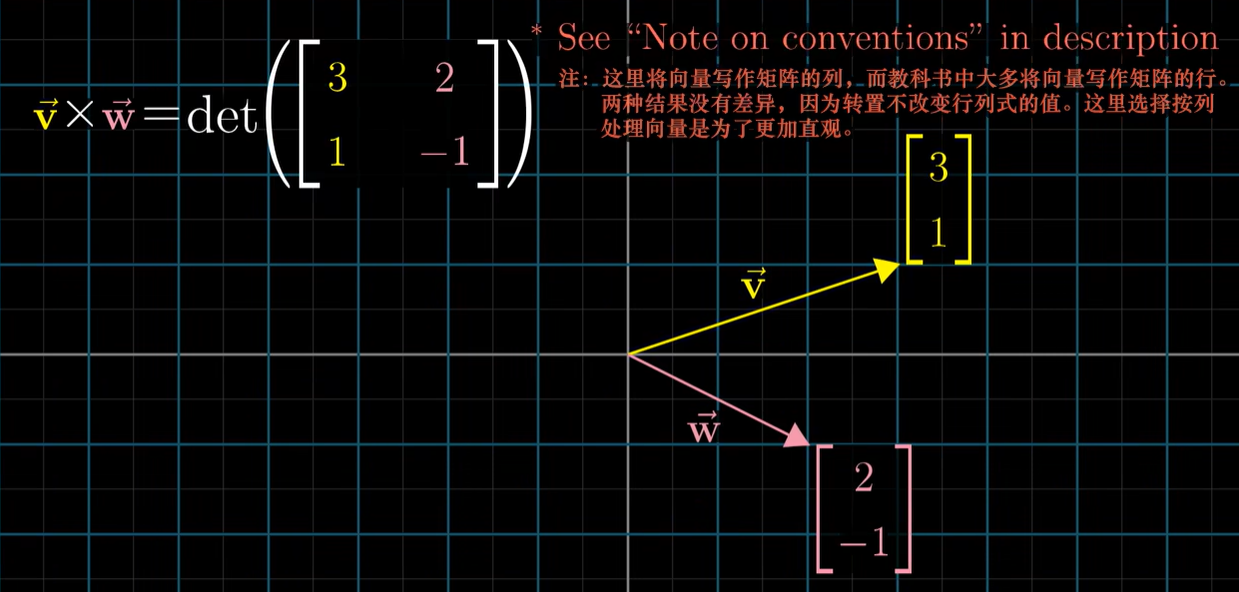
- 实际上,叉积的结果不是一个数,而是一个向量;

 该向量的指向遵循右手螺旋定则,即三维坐标系中z轴方向(x为v,y为w)
该向量的指向遵循右手螺旋定则,即三维坐标系中z轴方向(x为v,y为w)
- 几何意义:
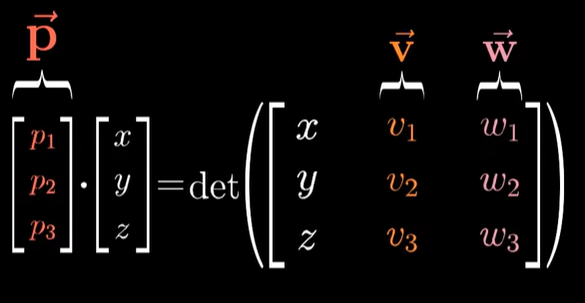 从点积出发,将任意三维向量投影到p上再与p的长度相乘,即该三维向量和v、w组成的平行六面体的体积;
根据平行六面体体积公式可以求出,p等同于垂直于v、w平面,长度为二者组成的平行四边形面积的向量
从点积出发,将任意三维向量投影到p上再与p的长度相乘,即该三维向量和v、w组成的平行六面体的体积;
根据平行六面体体积公式可以求出,p等同于垂直于v、w平面,长度为二者组成的平行四边形面积的向量
- 基变换
- 表达式 A−1MA 暗示一种数学上的转移作用:将b坐标系中的向量,用a坐标系的语言表达(A),再经过a坐标系的一次转换(M),最后翻译回b坐标系中的表达(A−1)
这是因为不管使用a坐标系还是b坐标系,表达的都是同一片空间
- 举例,如果 M 是a坐标系中的旋转矩阵,因为旋转在同一空间中是恒定的,则可以通过 A−1MA 得到b坐标系中的旋转矩阵
- 正交变换 Orthonormal Transformation
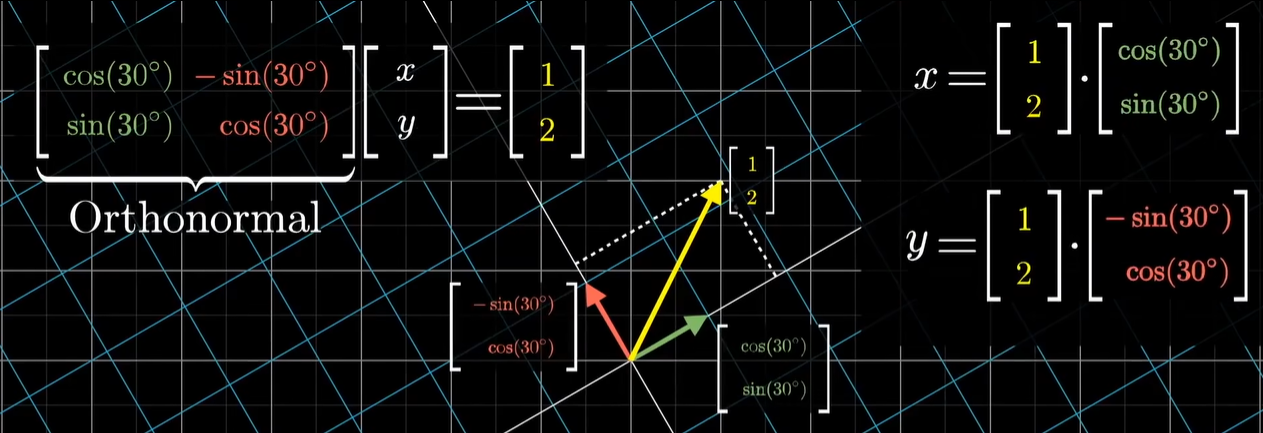
- 使基向量再变换后依然保持单位长度,且互相垂直,即 T(v)⋅T(w)=v⋅w
- ~ 特征向量 Eigenvectors
- 定义:在线性变换中仅被拉伸或压缩,而没有离开原本所在直线的向量
- 特征值 Eigenvalues
- 几何意义:用以理解一些变换,比如三维旋转的特征向量就是旋转轴
这里特征向量的特征值为1,因为旋转不涉及拉伸或者压缩
- 计算:
- Av=λv 相当于 (A−λI)v=0,求解非零 v
这代表着 A−λI 将空间压缩到了一个更低的维度
- det(A−λI)=0,得到特征值
空间压缩 = 非满秩 = 矩阵行列式为0
- 将特征值代入 (A−λI)v=0,得到特征向量
- 补充:
- 当特征值为实数,这是一种拉伸或压缩
- 当特征值为复数,一般对应于某种旋转
- 当特征值为1,是剪切
- 特征基 Eigenbasis
- 当基向量正好是特征向量的时候,即对角矩阵,非常便于计算
- 因此,使用基变换使特征向量作为基向量是便于计算的
- 抽象向量空间
数学中有很多类似向量的概念,只要该集合具有合理的数乘和相加概念,就可以使用线性代数
- 函数 = 向量

- 线性:线性变换保持向量加法运算和数乘运算 求导是一种线性运算
- 可加性 Additivity
- L(v+w)=L(v)+L(w)
- dxd(x3+x2)=dxd(x3)+dxd(x2)
- 成比例 Scaling
- L(cv)=cL(v)
- dxd(4x3)=4dxd(x3)
- 求导:线性运算
- 当前空间:全体多项式
- 基函数:1,x,x2,x3……
 基函数的集合是无穷大的,这说明当我们用向量表示一个函数,它的维度无限大
基函数的集合是无穷大的,这说明当我们用向量表示一个函数,它的维度无限大
- 求导矩阵:
 根据线性,这就是把所有基函数单独求导得到的向量拼接成的矩阵
根据线性,这就是把所有基函数单独求导得到的向量拼接成的矩阵
- 总结:
- 向量可以是任何东西
- 只要相加和数乘的概念遵循公理,都属于向量空间,可以使用线性代数的结论

- 克莱姆法则 Cramer’s rule
- 将坐标视作与基向量构成的有向面积/体积,在变换发生时,所有面积/体积的伸缩比例可以通过行列式得到
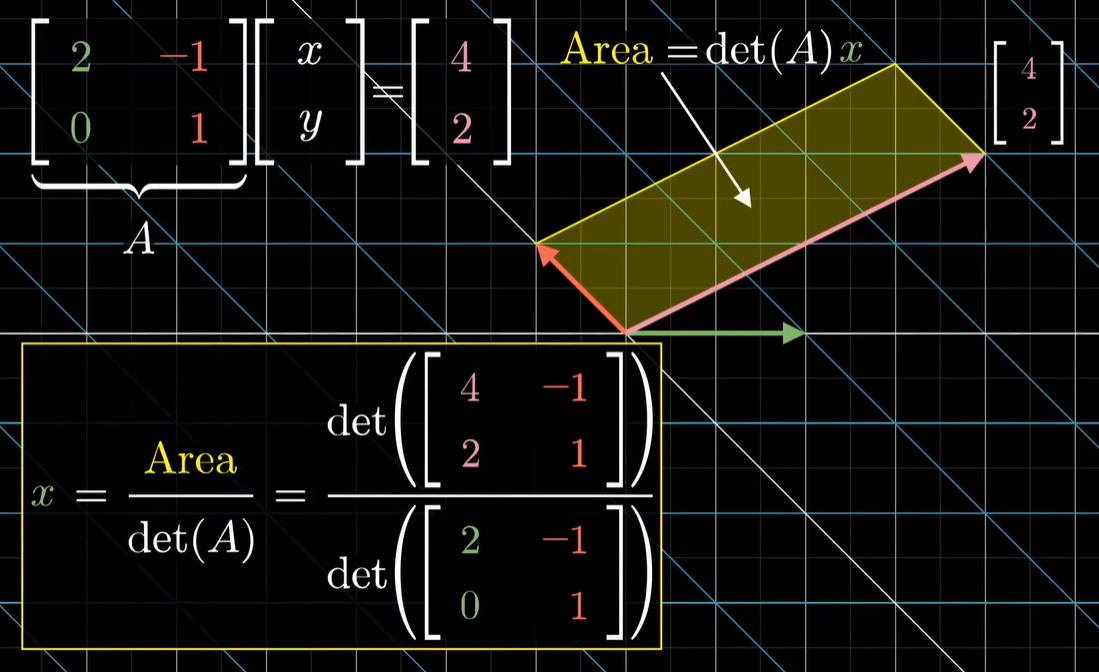
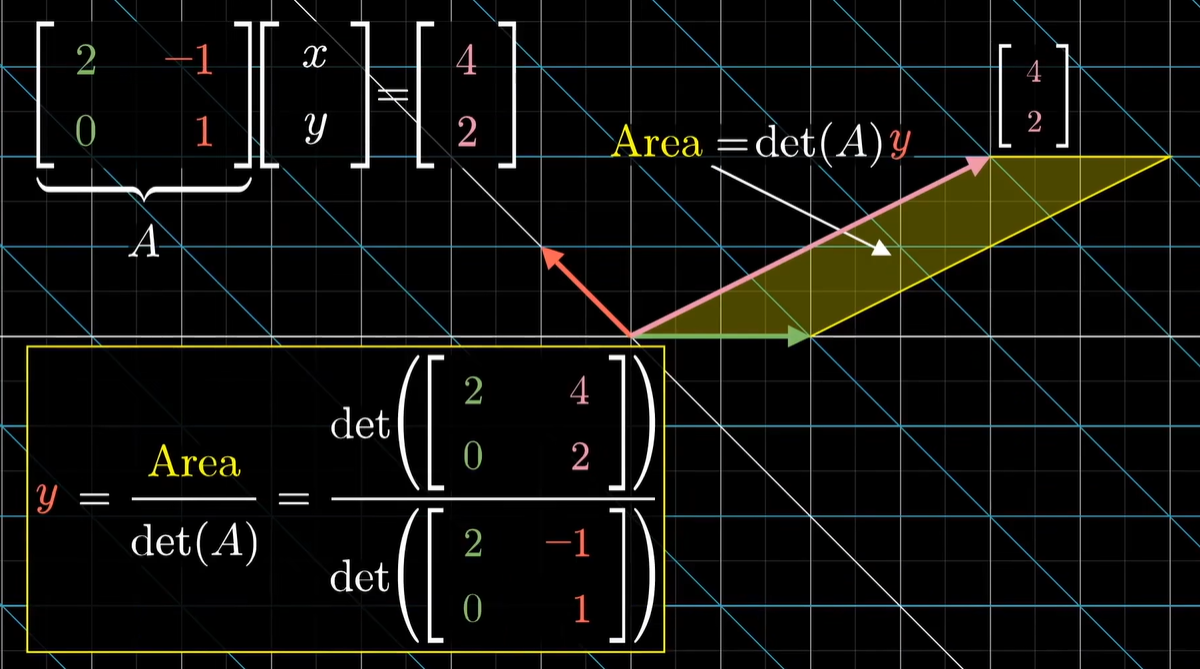
- 是 Ax=b 求解的一种直接方法,具体来说:x1=∣A∣∣b,a2∣, x2=∣A∣∣a1,b∣ x1=∣A∣∣b,a2,a3∣, x2=∣A∣∣a1,b,a3∣, x3=∣A∣∣b,a2,a3∣
- 然而,行列式计算的复杂度会随着 x 维度的变大而急剧上升,因此 matlab 等软件在计算是都采用高斯消元法,通过将增广矩阵尽可能化作上三角矩阵实现求解
- 奇异值分解 Singular Value Decomposition
- 形式:A=UΣVT,其中 A 是一个 m×n 的矩阵
- U:m×m 的矩阵,其列向量是左奇异向量,即 AAT 的特征向量 u1,u2,…,um
- Σ:m×n 的对角矩阵,对角线上的元素是奇异值 σ1,σ2,…,σr,其余位置为0
- 奇异值:将 ATA 的特征值取平方根,得到奇异值 σ1,σ2,…,σr,其中 r 是矩阵的秩
- V:n×n 的矩阵,其列向量是右奇异向量,即 ATA 的特征向量 v1,v2,…,vn
- 几何意义:A 可以看作是一个从 n-维空间到 m-维空间的线性变换。SVD 将这个复杂的线性变换分解为三个更简单的变换:旋转、维度缩放和再次旋转。
- 在 n-维空间中旋转(正交变换),使特征向量变为基向量,对应矩阵 VT
- 维度变化 + 缩放(对角变换),对应 Σ
- 在 m-维空间中旋转(正交变换),将特征向量还原、原基向量归位
- 补充:AAT 和 ATA 是半正定对称矩阵
- 对称矩阵的特征向量是相互垂直的
- 正交矩阵有一个重要性质,即其转置矩阵和逆矩阵相等,这也是正交矩阵的定义
- 二者的特征值相同
- 可以正交对角化: A⊤A=VΛV⊤,AA⊤=UΛ′U⊤
- 其中 V,U 是正交矩阵,Λ,Λ′ 是对角矩阵,且非负
- Λ,Λ′ 即特征值组成的对角矩阵,非零部分相同
- Λ=Σ2
- 则有:
- A⊤A=VΛV⊤
- A⊤AV=VΛ=VΣ2
- AV=UΣ 这一步是因为 V 和 U 之间有一些奇妙的联系
- A=UΣV⊤
Reference

 对于单一矩阵乘以向量,左乘变换行,右乘变换列
对于单一矩阵乘以向量,左乘变换行,右乘变换列 将两个函数复合时,需要从右向左读 —— f(g(x)),矩阵也一样
将两个函数复合时,需要从右向左读 —— f(g(x)),矩阵也一样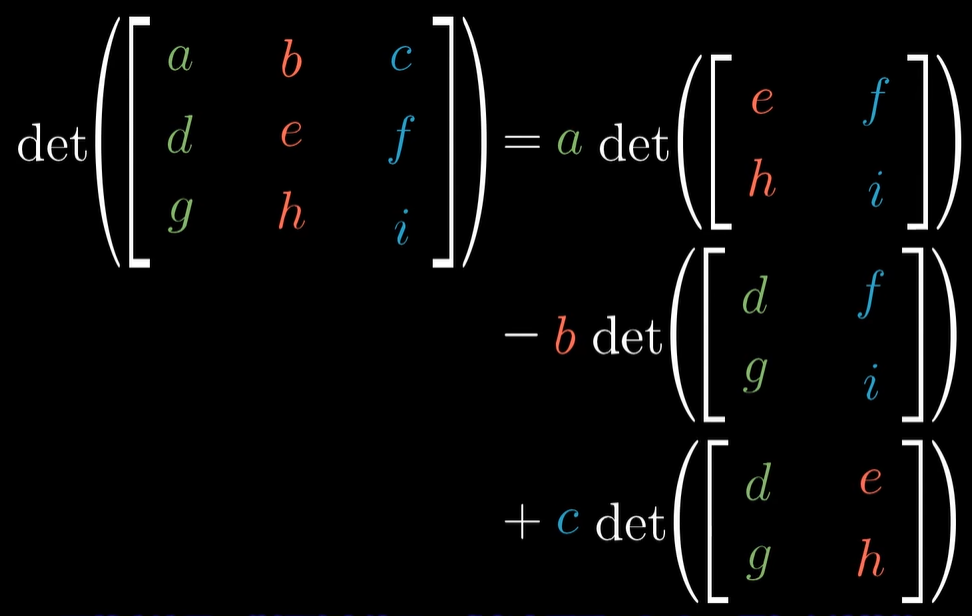
 将一个二维向量投影到一个一维空间,这个变换用 矩阵来描述,且该一维空间就是该矩阵转置得到的向量所在的数轴
因此,可以通过投影长度相乘来计算点积
将一个二维向量投影到一个一维空间,这个变换用 矩阵来描述,且该一维空间就是该矩阵转置得到的向量所在的数轴
因此,可以通过投影长度相乘来计算点积

 该向量的指向遵循右手螺旋定则,即三维坐标系中z轴方向(x为v,y为w)
该向量的指向遵循右手螺旋定则,即三维坐标系中z轴方向(x为v,y为w)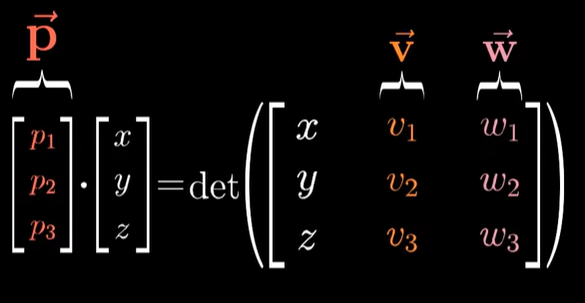 从点积出发,将任意三维向量投影到p上再与p的长度相乘,即该三维向量和v、w组成的平行六面体的体积;
根据平行六面体体积公式可以求出,p等同于垂直于v、w平面,长度为二者组成的平行四边形面积的向量
从点积出发,将任意三维向量投影到p上再与p的长度相乘,即该三维向量和v、w组成的平行六面体的体积;
根据平行六面体体积公式可以求出,p等同于垂直于v、w平面,长度为二者组成的平行四边形面积的向量

 基函数的集合是无穷大的,这说明当我们用向量表示一个函数,它的维度无限大
基函数的集合是无穷大的,这说明当我们用向量表示一个函数,它的维度无限大 根据线性,这就是把所有基函数单独求导得到的向量拼接成的矩阵
根据线性,这就是把所有基函数单独求导得到的向量拼接成的矩阵

