正向运动学

3 most important points

1. 正向运动学的目的是对机器人末端的位姿进行建模，由 6 个参数组成
2. 经典 DH 参数
3. 变换矩阵公式

5 thoughts

1. 显然改进 D-H 参数法用的比较多
2. 如果两个 z 轴在一点相交，那么一般把两个坐标系都放在交点处
3. 如果两个 z 轴共线，那么可以合并

Notes

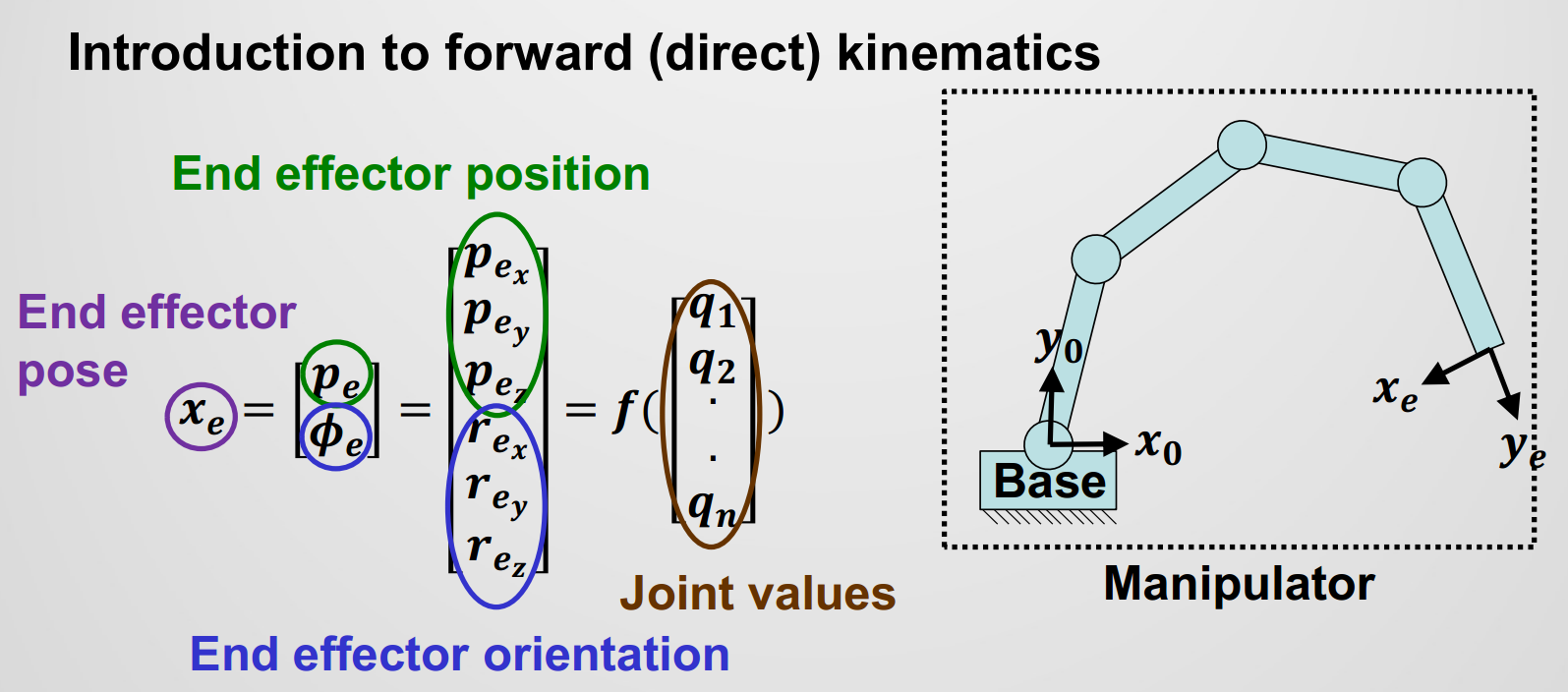
• 目的是对末端效应器的位姿进行建模
  • 位置（3 个参数）
  • 姿态（3 个参数）

Example

自由度与运动副

自由度

在三维空间中，一个刚体（比如一个连杆）最多拥有 6 个自由度。

• 3 个平移自由度：沿着三个互相垂直的坐标轴（例如 X, Y, Z 轴）进行直线运动。
• 3 个旋转自由度：绕着这三个互相垂直的坐标轴进行旋转运动。

这就像一个在空中自由飞行的无人机：

• 它可以向前/后、左/右、上/下移动（3 个平移）。
• 它可以俯仰、偏航、滚转（3 个旋转）。

然而，一个有 6 个自由度为 1 的关节的机械臂，其总自由度（即末端执行器在空间中的独立运动数目）取决于这 6 个关节的类型和它们的轴线在空间中的排列方式。

• 在精心设计的、非奇异的构型下，它的自由度是6。
• 如果关节轴线排列导致运动冗余或奇异性，它的有效自由度会小于 6。

• Links 从 base 开始标号，base 为 0，末端为 $n$
• Joints 从 1 开始标号，分别关联 link $i$ 和 $i-1$
  • Lower Pair：指的是两个构件之间面接触的运动副
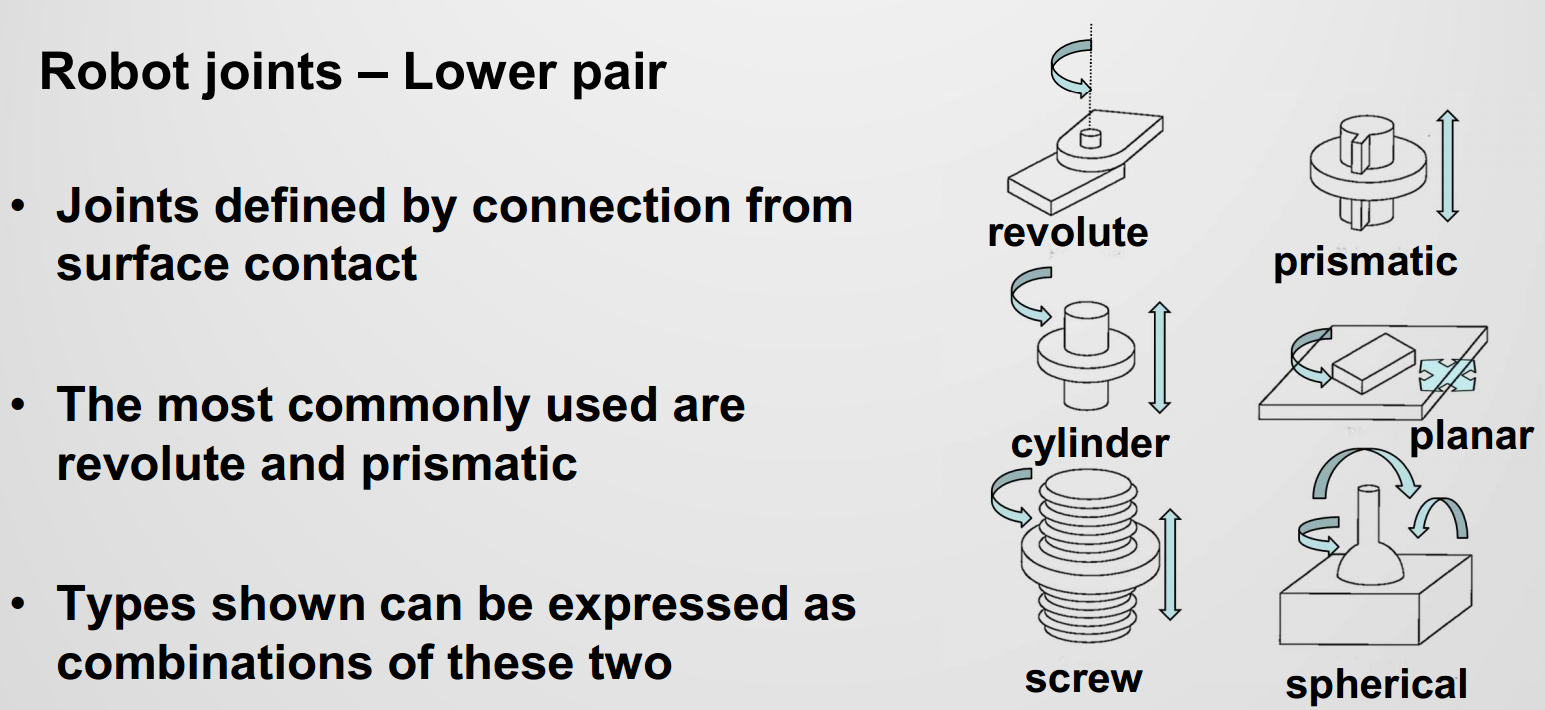
  • Higher Pair：指的是两个构件之间点接触或线接触的运动副

特征	Higher Pair（高副）	Lower Pair（低副）
接触形式	点接触 或 线接触	面接触
自由度 (相对)	相对较多，约束较少	相对较少，约束更多
接触压强	高（因为接触面积小）	低（因为接触面积大）
磨损与寿命	更容易磨损，寿命较短	更耐磨，寿命较长
常见例子	齿轮副（齿与齿是点/线接触） 凸轮与从动件（点/线接触） 滚动轴承（滚珠与轨道是点接触） 火车车轮与钢轨（理论上为线接触）	旋转副/铰链（如门合页，圆柱面接触） 移动副/棱柱副（如活塞与气缸，面接触） 球面副（如球铰，球面接触） 螺旋副（如螺丝与螺母，螺纹面接触）
直观比喻	踩高跷：高跷与地面是点接触，不稳定，压强大。 两个玻璃球相碰	穿平底鞋站立：鞋底与地面是面接触，稳定，压强小。 抽屉在柜体里滑动

D-H 参数法

• 全名：Denavit-Hartenberg Convention
• 价值：
  • 想象一个机器人手臂由一系列连杆和关节组成。要描述末端执行器在空间中的位置和姿态，最直接的方法是为每个连杆建立一个坐标系。但如何建立这些坐标系？它们之间的关系又如何描述？
  • D-H 方法通过一套严格的规则解决了这个问题，确保每个相邻坐标系之间的变换都可以用仅有的 4 个参数 来表示。

经典 D-H 参数

参数	符号	描述
连杆长度	$a_{i-1}$	从关节轴 i-1 到关节轴 i 的公垂线距离。可以理解为连杆的“长度”。
连杆扭角	${\alpha }_{i-1}$ ​	绕关节轴 i-1 和关节轴 i 之间的公垂线，将轴 i-1 旋转到与轴 i 平行所需的角度。可以理解为连杆的“扭曲”程度。
连杆偏距	$d_i$ ​	沿关节轴 i 的方向，从连杆 i-1 的坐标系原点移动到与关节轴 i 的公垂线交点处的距离。对于移动关节，这是一个变量。
关节角	${\theta }_i$	绕关节轴 i，将连杆 i-1 的 X 轴旋转到与连杆 i 的 X 轴平行所需的角度。对于旋转关节，这是一个变量。

• 在这 4 个参数中，只有 1 个是变量：
  • 如果是旋转关节，则 ${\theta }_i$ 是变量。
  • 如果是移动关节，则 $d_i$ 是变量。
• 其余 3 个参数是由机器人机械结构的物理尺寸决定的常量。

• 建模步骤
  1. 建立坐标系：按照 D-H 规则，为每个连杆分配一个坐标系（Z 轴沿关节轴，X 轴沿公垂线方向）。
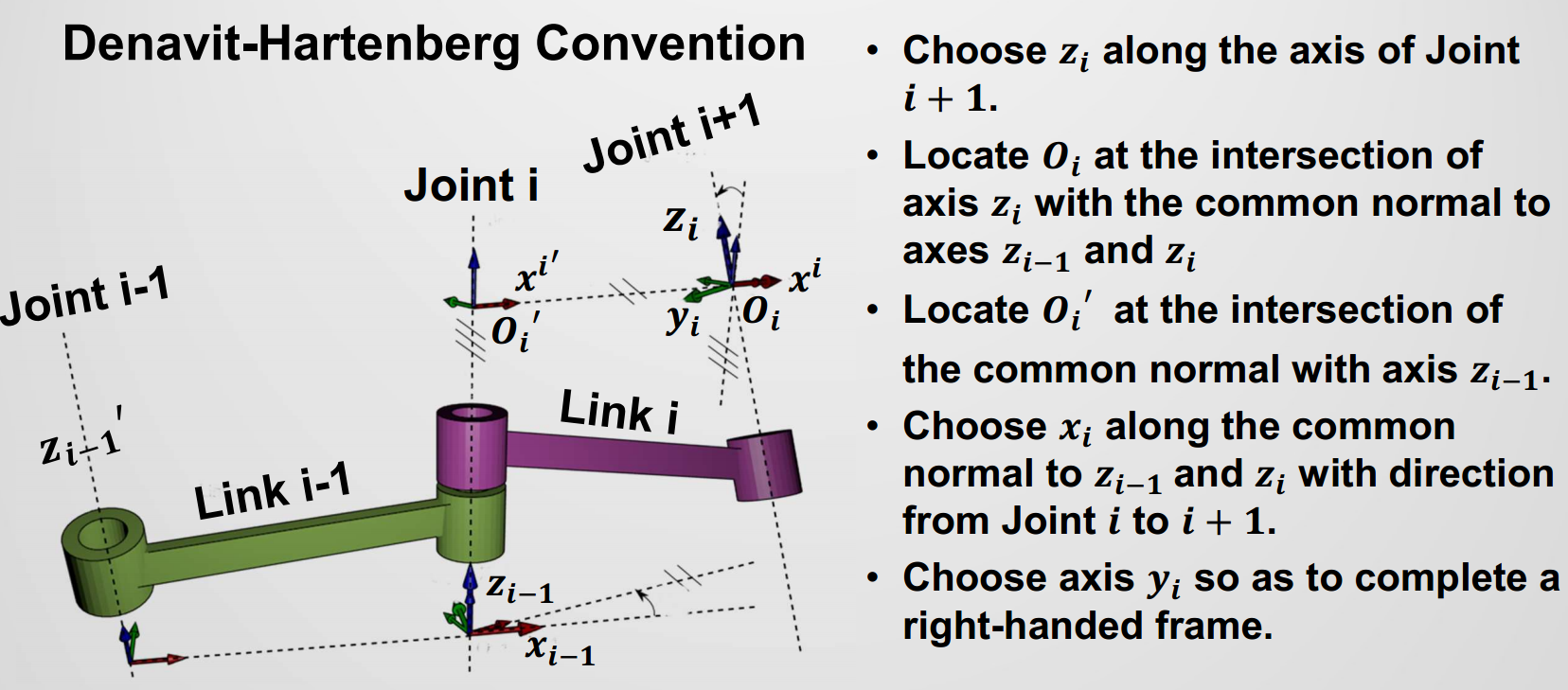
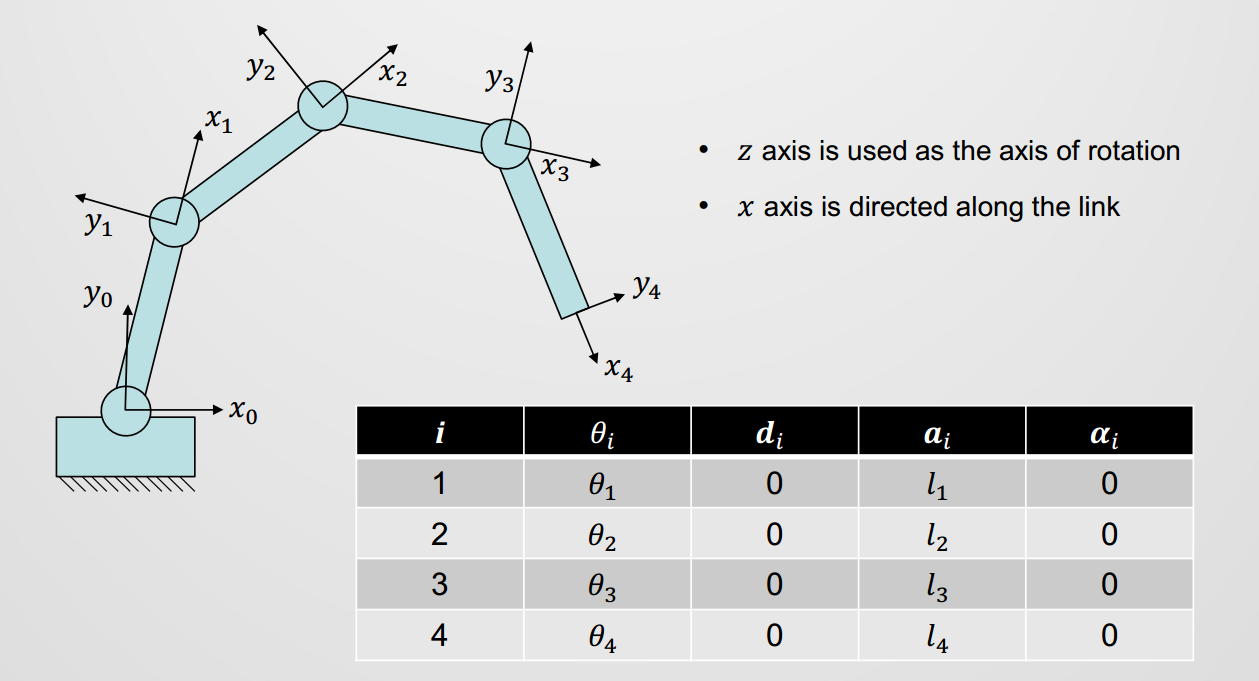
  2. 确定参数：根据机械结构，为每一对相邻的连杆确定 4 个 D-H 参数 $(a_{i-1},{\alpha }_{i-1},d_i,{\theta }_i)$。
  3. 构建变换矩阵：利用这 4 个参数，可以写出一个标准的 $4\times 4$ 齐次变换矩阵，该矩阵描述了如何将坐标系 i 变换到坐标系 i-1。
  4. 计算总变换：将所有的连杆变换矩阵连乘起来，就能得到从机器人基座（坐标系 0）到末端执行器（坐标系 n）的总变换矩阵；就是机器人的运动学方程，它包含了末端执行器的位置和姿态信息，是所有运动控制的基础。

变换矩阵公式

$$\begin{array}{rl}{}^{i-1}{T}_i& =Tran{s}_{z_{i-1}}(d_i)Ro{t}_{z_{i-1}}({\theta }_i)Tran{s}_{x_i}(a_i)Ro{t}_{x_i}({\alpha }_i)\\ & =\left[\begin{array}{cccc}\cos ({\theta }_i)& -\sin ({\theta }_i)\cos ({\alpha }_i)& \sin ({\theta }_i)\sin ({\alpha }_i)& a_i\cos ({\theta }_i)\\ \sin ({\theta }_i)& \cos ({\theta }_i)\cos ({\alpha }_i)& -\cos ({\theta }_i)\sin ({\alpha }_i)& a_i\sin ({\theta }_i)\\ 0& \sin ({\alpha }_i)& \cos ({\alpha }_i)& d_i\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

以上矩阵均为齐次变换矩阵

连乘得到总变换公式（平面）：

$${}^0{T}_n{=}^0{T}_1^1{T}_2..{.}^{n-2}{T}_{n-1}^{n-1}{T}_n=\left[\begin{array}{cccc}\cos \Theta & -\sin \Theta & 0& {\sum }_{i=1}^n{l}_i\cos {\varphi }_i\\ \sin \Theta & \cos \Theta & 0& {\sum }_{i=1}^n{l}_i\sin {\varphi }_i\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

其中：

$$\Theta =\sum _{i=1}^n{\theta }_i,{\varphi }_i=\sum _{k=1}^i{\theta }_k$$

Modified D-H 参数法

改进 D-H 参数法，也常被称为 Craig’s Modified D-H 参数法，是对标准 D-H 参数法的一种优化。它通过微调坐标系附着的方式，在处理某些类型的机器人时（特别是树状或带闭链的机构）更为直观和方便，并且在动力学分析中更具优势。

核心思想：坐标系附着点的改变

• 标准 D-H：将坐标系 {i} 附着在连杆 i 的远端（即靠近下一个关节 i+1 的一端）。
• 改进 D-H：将坐标系 {i} 附着在连杆 i 的近端（即靠近自身关节 i 的一端）。

在改进 D-H 法中，四个参数是围绕同一个坐标系 {i} 和同一个关节轴 i 来定义的，这使得定义更加统一和直观。

改进 D-H 参数

对于连杆 i 和关节 i，其参数定义如下：

参数	符号	描述	围绕的轴
连杆长度	$a_i$	从关节轴 i 到关节轴 i+1 的公垂线距离。	X 轴
连杆扭角	${\alpha }_i$	绕 $X_i$ 轴，将关节轴 i 旋转到与关节轴 i+1 平行所需的角度。	X 轴
连杆偏距	$d_i$	沿 $Z_i$ 轴（关节轴 i），从 $X_{i-1}$ 轴移动到 $X_i$ 轴的距离。	Z 轴
关节角	${\theta }_i$	绕 $Z_i$ 轴（关节轴 i），从 $X_{i-1}$ 轴旋转到 $X_i$ 轴所需的角度。	Z 轴

• 所有参数都与坐标系 {i} 相关联。
• 同样，只有 1 个是变量：
  • 如果是旋转关节，则 ${\theta }_i$ 是变量。
  • 如果是移动关节，则 $d_i$ 是变量。

• 改进 D-H 的坐标系建立步骤
  1. 确定 Z 轴：$Z_i$ 轴沿关节 $i+1$ 的轴线方向。
  2. 确定原点：原点 $O_i$ 是 $Z_i$ 轴和 $Z_{i+1}$ 轴的公垂线与 $Z_i$ 轴的交点。
  3. 确定 X 轴：$X_i$ 轴沿 $Z_i$ 轴和 $Z_{i+1}$ 轴的公垂线方向，从关节 $i$ 指向关节 $i+1$。
  4. 确定 Y 轴：通过右手定则，由 $Z_i$ 和 $X_i$ 确定 $Y_i$ 轴。
• 示意图：

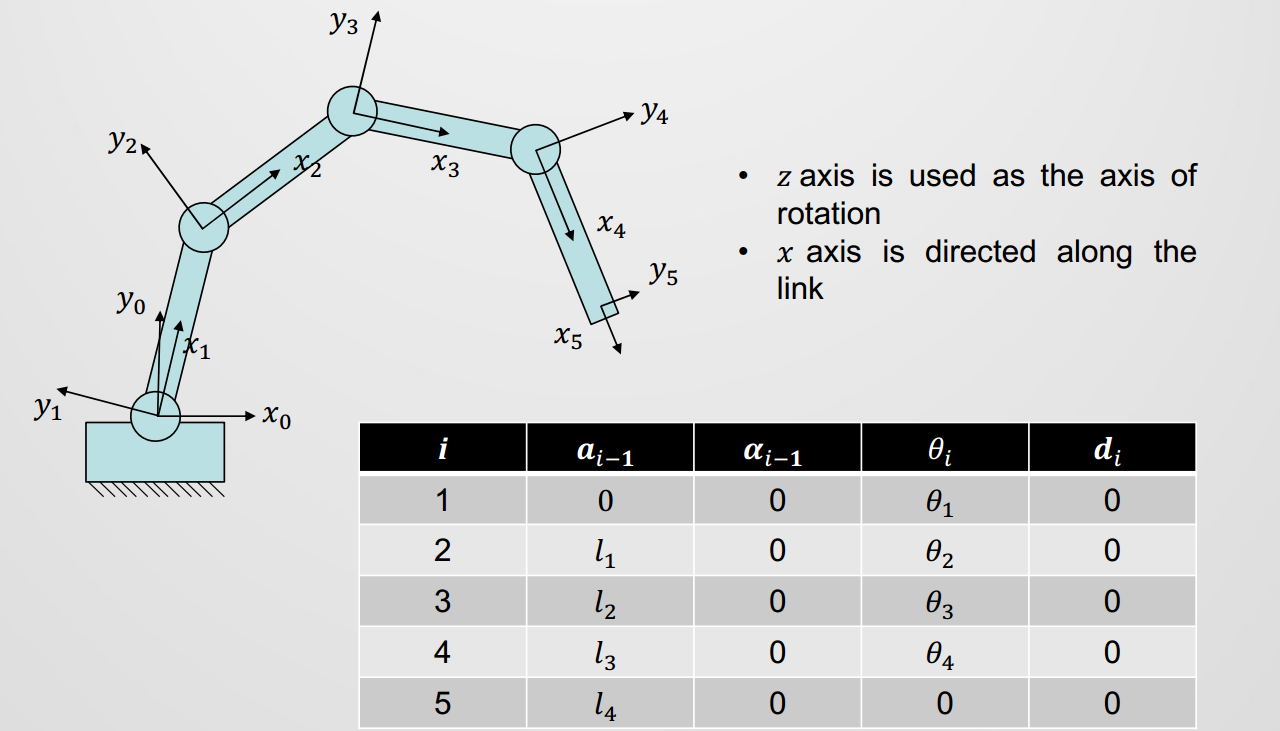
变换矩阵公式

${}^{i-1}{T}_i=Ro{t}_{x_{i-1}}({\alpha }_{i-1})Tran{s}_{x_{i-1}}(a_{i-1})Ro{t}_{z_i}({\theta }_i)Tran{s}_{z_i}(d_i)$

对比

让我们用一个简单的旋转连杆来对比：

特性	标准 D-H	改进 D-H
坐标系位置	附着在连杆远端	附着在连杆近端
参数关联	参数在连杆 i-1 和关节 i 之间“混合”	所有参数都与连杆 i 和关节 i 清晰关联
变换直观性	稍差，参数定义跨越连杆	更直观，所有操作都围绕当前坐标系进行
动力学应用	较不方便	更方便，因为坐标系固定在连杆本体上，惯性张量定义更自然
普及度	传统、经典，在很多教科书中使用	在现代机器人工具箱（如 Robotics Toolbox for MATLAB）中更常用
改进 D-H 法的优点：

1. 直观性：参数定义全部围绕同一个坐标系，物理意义更清晰。
2. 动力学友好：坐标系固定在连杆上，极大地简化了连杆质心、惯性张量等动力学参数的定义。
3. 编程方便：其统一的变换流程更容易在代码中实现。

指数积法 Product of Exponentials (PoE)

Warning

具体推导过程见课件 4- Jacobian and Differential Kinematics

• 核心思想
  • 只使用两个坐标系：只需要建立基座坐标系 $B$ 和末端执行器坐标系 $T$，无需像 D-H 法那样为每个连杆建立坐标系。
  • 运动链视为一系列刚体运动的“指数”相乘：将机器人从基座到末端的整体变换，表示为各个关节运动（以指数形式表示）的乘积。
  • 基于旋量理论：该方法建立在李群李代数的旋量理论之上，数学上非常优雅。

与 D-H 参数法的直观对比

特性	D-H 参数法	指数积法
坐标系数量	每个连杆一个坐标系	仅需两个坐标系（基座和末端）
建模思路	几何参数化：通过相邻连杆的几何关系（a, α, d, θ）一步步推导	运动叠加：将每个关节的运动（旋量 $S_i$) 直接以指数形式相乘
计算基础	齐次变换矩阵连乘	矩阵指数的连乘
优点	直观，易于理解，有标准步骤	公式统一，无奇异性问题，特别适合速度级运动学和动力学分析
缺点	对于复杂结构（如并联、闭链）建模困难	数学抽象，需要李群李代数基础

• 核心公式：${}^0{g}_n=e^{[S_1]q_1}{e}^{[S_2]q_2}...e^{[S_n]q_n}g(0)$

  • $g(0)$：
    • 这是机器人的“零位构型”。
    • 表示当所有关节变量 $q_i=0$ 时，末端坐标系相对于基座坐标系的齐次变换矩阵。
    • 它是一个常数矩阵，描述了机器人的初始姿态。
  • $S_i$（运动旋量）：
    • 这是指数积法的核心参数。
    • 它是一个 $4\times 4$ 的矩阵，封装了第 $i$ 个关节的运动轴信息。
    • 其形式为：$S_i=\left[\begin{array}{cc}[{\omega }_i]& v_i\\ 0& 0\end{array}\right]$
      • 其中：
        • $[{\omega }_i]$ 是一个 $3\times 3$ 的反对称矩阵，代表了关节旋转轴的方向。实际上是角速度
        • $v_i$ 是一个 $3\times 1$ 的向量，与关节的位置有关。对于旋转关节，它包含了轴上任意一点的信息；对于移动关节，它表示移动的方向。
  • $e^{[S_i]q_i}$（矩阵指数）：
    • 这代表了第 i 个关节运动 $q_i$（角度或位移）所对应的刚体变换。
    • 它计算的是一个齐次变换矩阵，描述了由关节 i 的运动所引起的刚体位移。

• 运动旋量 $S_i$ 的深入理解

  • 反对称矩阵 $[\omega {]}_{\times }$： 它将一个三维向量 $\omega =({\omega }_x,{\omega }_y,{\omega }_z{)}^T$ 转化为一个反对称矩阵，用于表示叉乘运算：$[\omega {]}_{\times }=\left[\begin{array}{ccc}0& -{\omega }_z& {\omega }_y\\ {\omega }_z& 0& -{\omega }_x\\ -{\omega }_y& {\omega }_x& 0\end{array}\right]$

  • 运动旋量 $S_i$：$S_i=\left[\begin{array}{cccc}0& -{\omega }_z& {\omega }_y& v_x\\ {\omega }_z& 0& -{\omega }_x& v_y\\ -{\omega }_y& {\omega }_x& 0& v_z\\ 0& 0& 0& 0\end{array}\right]$ 它由 $[\omega {]}_{\times }$ 和 $v$ 组合而成。

矩阵指数的计算（罗德里格斯公式）

计算 $e^{[S_i]q_i}$ 中旋转部分和平移部分的公式，实际上是罗德里格斯公式在旋量表示下的形式。

对于一个旋转关节（$||\omega ||=1$，$q_i={\theta }_i$）：

• 旋转部分 $R_i$： $R_i=e^{[\omega {]}_{\times }{\theta }_i}=I+\sin {\theta }_i[\omega {]}_{\times }+(1-\cos {\theta }_i)[\omega {]}_{\times }^2$ 这个公式可以直接计算绕轴 $\omega$ 旋转 $\theta$ 角后的旋转矩阵。

• 平移部分 $d_i$： $d_i=\left(I+\frac{1-\cos {\theta }_i}{{\theta }_i^2}[\omega {]}_{\times }+\frac{{\theta }_i-\sin {\theta }_i}{{\theta }_i^3}[\omega {]}_{\times }^2\right)v$ 这个公式计算了由于旋转和平移耦合效应产生的位移。

• 重要性
  1. 统一性：对于旋转关节和移动关节，公式形式完全统一，无需区分。
  2. 数值稳定性：避免了 D-H 法中在奇异构型附近可能出现的数值问题。
  3. 速度级运动学直接相关：运动旋量 $S_i$ 直接对应于雅可比矩阵的列，使得速度分析和控制更加直接。
  4. 现代机器人学的基石：它是理解机器人动力学、优化控制和现代几何机器人理论的基础。

Related

• 位姿
• 坐标变换

Reference