3 most important points
- Value-based 方法输出 Q;Policy-based 方法输出动作概率
- Value-based 多为确定性策略,但被限制于离散动作空间;Policy-based 多为随机性策略,更适合连续动作空间。但 DDPG 实现了以确定性策略输出到连续动作空间,非常适合低层控制。
- PPO 的核心点包括重要性采样和 clip。重要性采样实现无偏估计,同时实现对旧数据的复用,提高样本效率;clip 控制重要性采样带来的高方差,提高训练稳定性,且计算简单。因而,样本效率高、计算简单、训练稳定使 PPO 成为最流行的算法之一。
5 thoughts
- Actor-Critic 不是“两种方法的简单拼接”,而是使用 Critic 优势函数对策略梯度进行方差控制
- 基线(优势函数)的引入相当于一种奖励正则化,将奖励分布“平移”到均值为 0 附近,从绝对值到相对值,这样可以提高训练稳定性
- 对策略梯度算法的改进,主要针对的就是限制参数迭代的这一步,以防止策略发生过度漂移
- 一般来说 TD 优于 MC?TD 训练稳定但不精确,MC 精确但不稳定;但很多现实问题没有清晰的”回合结束”,MC 不适用;多步 TD 是折中的方案。
- “On-policy vs Off-policy” 的本质是数据重用性与稳定性之间的权衡。Off-policy(如 DQN)能复用历史数据(经验回放),样本效率高,但目标策略与行为策略不一致会引入偏差,训练更不稳定;On-policy(如 REINFORCE)数据只能用一次,样本效率低,但更新更稳定、理论更干净。PPO 之所以流行,正是因为它在 On-policy 框架下通过重要性采样近似实现了有限的数据重用,取得了平衡。
Notes
Abstract
特性 DQN REINFORCE DDPG A3C PPO 更新方式 单步 TD 回合 MC 单步 TD 多步 TD 多步 TD(GAE) 样本利用率 高 低 高 低-中 中(有限数据重用) 训练稳定性 中偏低 低 中偏低 中 高 并行能力 低 中 低 高(异步) 高(同步并行) 适用场景 离散动作 简单任务 连续控制 中等任务 各种任务(主流基线)
基础
- MDP 四元组<S, A, P, R> 马尔科夫决策过程
- S:state
- A:action
- R:reward
- P:probability 状态转移概率,即 action 后进入下一 state 的概率
- 动作空间
- 连续
- 速度
- 角度
- 电流
- 离散
- 连续
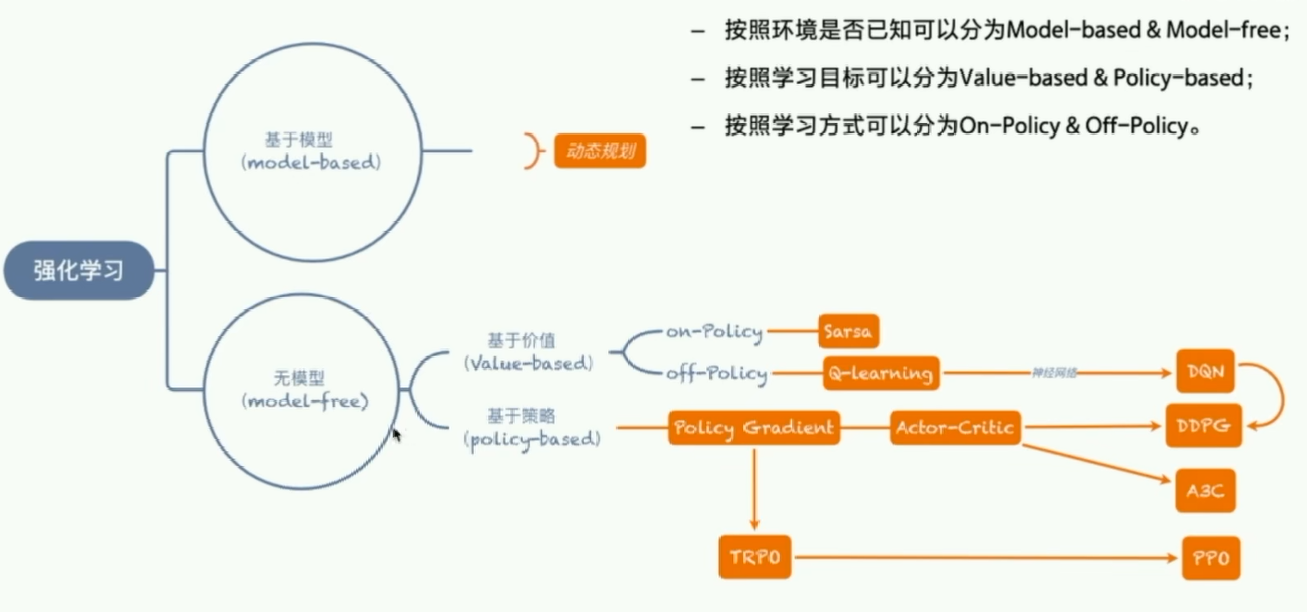
- 强化学习分类
- 环境
- Model-based:P 函数和 R 函数已知
- & Model-free:P 函数和 R 函数未知
- 学习目标
- Value-based:
- 状态价值驱动,通过 Q 间接求 action
- 确定性策略(目标导向)
- 常输出到离散动作空间
- Policy-based:
- 动作概率驱动,reward 判断,直接求 action
- 随机性策略
- 常输出到连续动作空间
- Value-based:
- 学习方式
- On-policy:
- 行为策略(收集数据)与目标策略(优化目标)是同一个策略
- 从 采样数据,用来优化
- Off-policy:
- 行为策略(收集数据)与目标策略(优化目标)是不同策略
- 从 采样数据,用来优化 (其中 )
- On-policy:
- 环境
确定性与随机性
- Valued-based 方法在确定参数之后,输入同一状态,得到的是同一个 action
- Policy-based 方法输出每个 action 的概率,可以根据概率得到不同 action
- 比如说,玩石头剪刀布,Valued-based 方法可能只会出剪刀,而 Policy-based 方法优化后会得到石头、剪刀、布各 33%,概率均等。
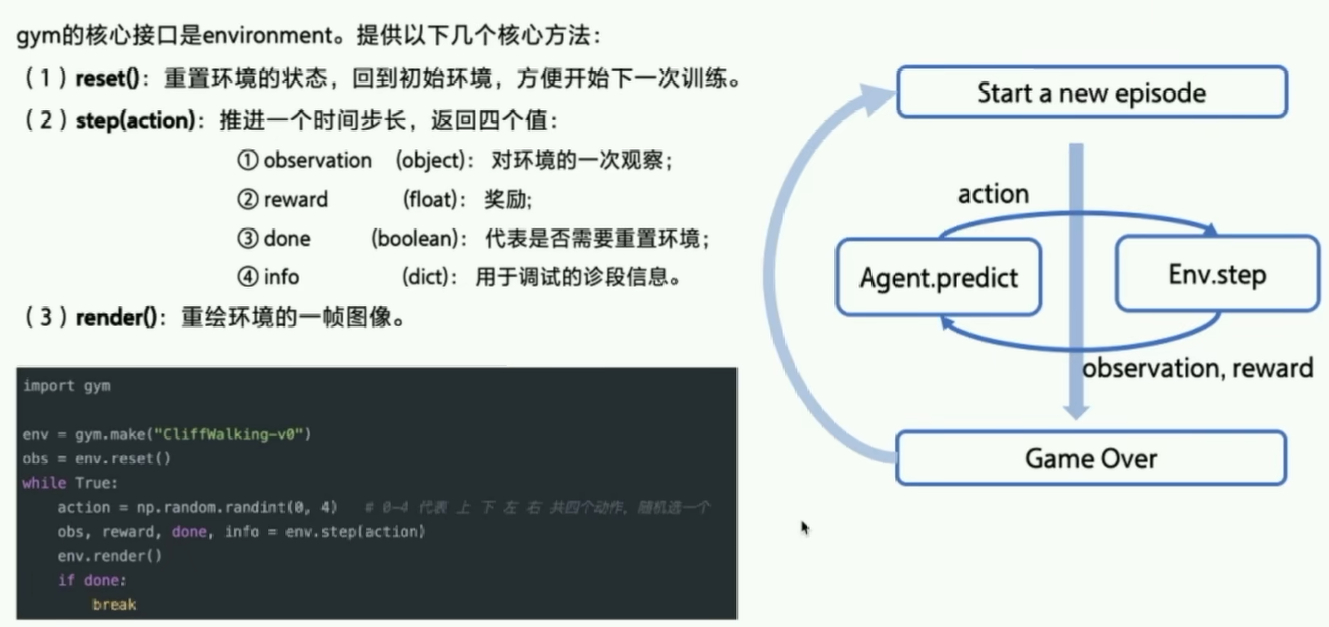
- 环境交互:Gym 为例
- 概念
- V:某个 state 的价值;存在 reward(价值)的状态会强化前一个 state 的价值 理解为非条件反射和条件反射,最后形成多级条件反射
- Q:状态动作价值,即在 state 时某个 action 的价值
- Target:未来收益之和,即后续 n 个状态的 reward 累加,以衰减因子 调控
- 更新:
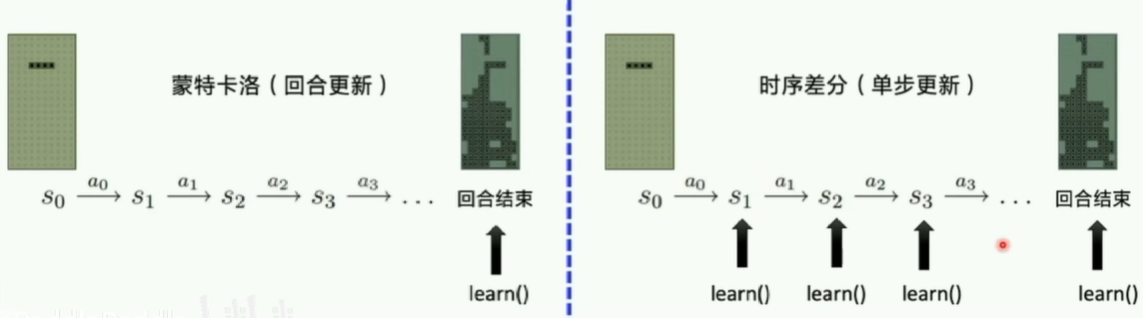
- 时序差分 Temporal Difference (TD),即单步更新
- 蒙特卡洛 Monte-Carlo (MC),即回合更新
Sarsa / Q-learning
核心思想
计算 Q 值并以表格形式存储,以此作为策略依据
- Sarsa:
- 分类:On-policy / Value-based
- 输入:
- Target:
- 更新:
- 过程:
sample -> step -> sample -> learn
- Q-learning:
- 分类:Off-policy / Value-based
- 输入:
- Target:
- 更新:
- 过程:
sample -> step -> learn
DQN
核心思想
- 问题:Q 表格缺陷
- 维度灾难:状态或动作空间稍大,表格就爆炸式增长,内存无法承受
- 查表效率低 / 无法扩展:即使内存够,访问稀疏表格效率低下,尤其在高维连续状态空间中几乎不可行
- 无泛化能力:每个状态-动作对独立学习,即使两个状态非常相似(如图像相差一个像素),Q 表也无法共享信息,导致学习效率极低、样本利用率差
- 解决:
- 使用 Q 函数逼近 Q 表格,即使用神经网络代替 Q-learning 中的 Q 表格
- 实现参数紧凑表示、状态泛化
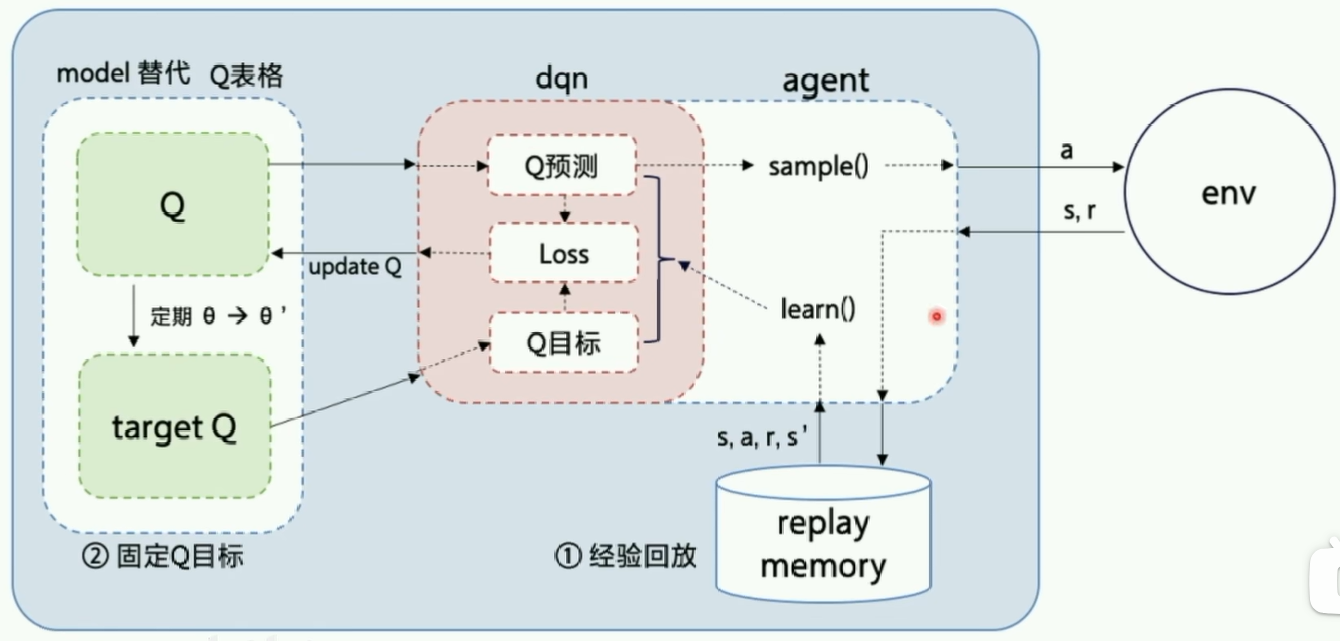
DQN 架构图
- 分类:Off-policy / Value-based
- 输入:
- 更新:损失函数 前一项是 Target 计算得到的真实值,后一项是预测值
- 创新点:
- 经验回放 Replay
- 方法
- 存储经验,也就是输入
- 随机选取一个 batch 的经验来更新表格 训练时所有输入都走回放
- 好处
- 提高样本利用率
- 打乱状态之间的时间相关性 迫使神经网络从“应试”到灵活应用
- 方法
- 固定 Q 目标
- 方法
- 固定一个 Q’ 网络,专门用于 Target
- 隔一段时间从 Q 更新 Q’ 参数
- 好处
- Target 不随 Q 变化,利于训练,算法平稳
- 方法
- 经验回放 Replay
- 代码结构:
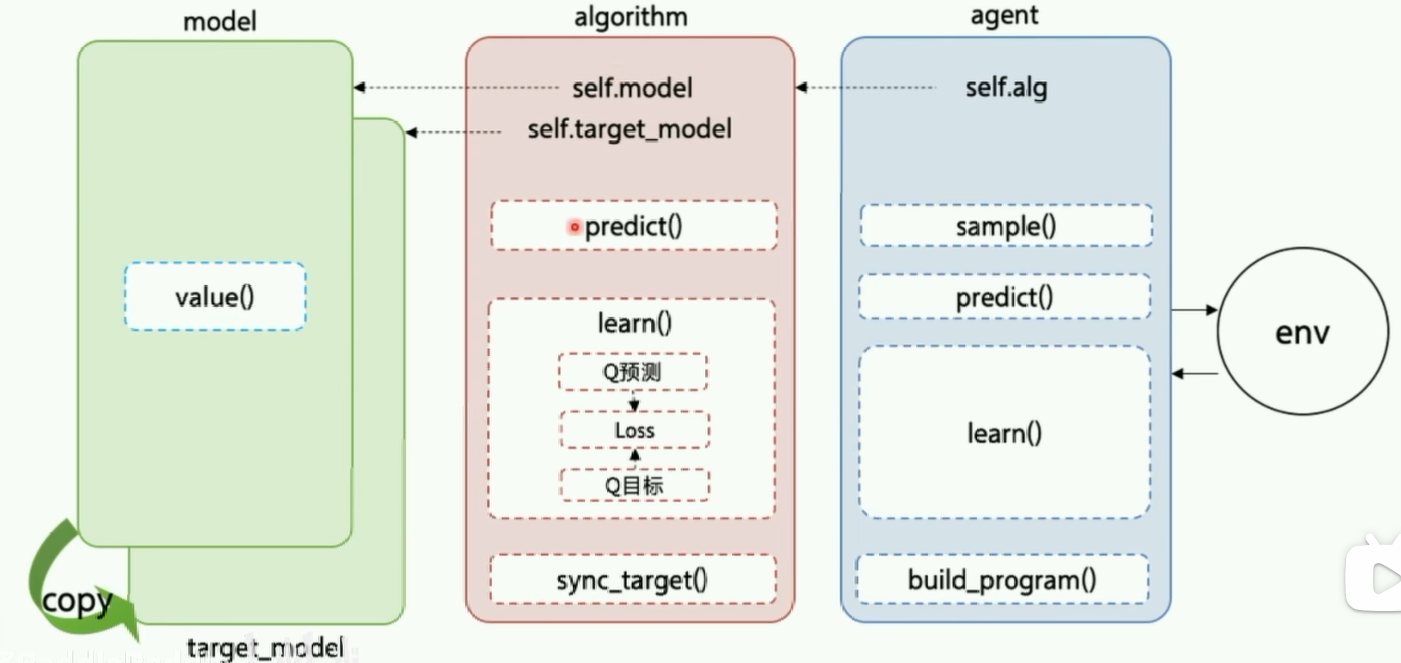
agent.pyalgorithm.pymodel.pyreplay_memory.pytrain.py
REINFORCE
核心思想
- 问题:
- DQN 不能用于连续动作空间
- 解决:
- 引入策略梯度,输出动作概率
- 一个 Episode 视为一个轨迹,直接优化策略函数
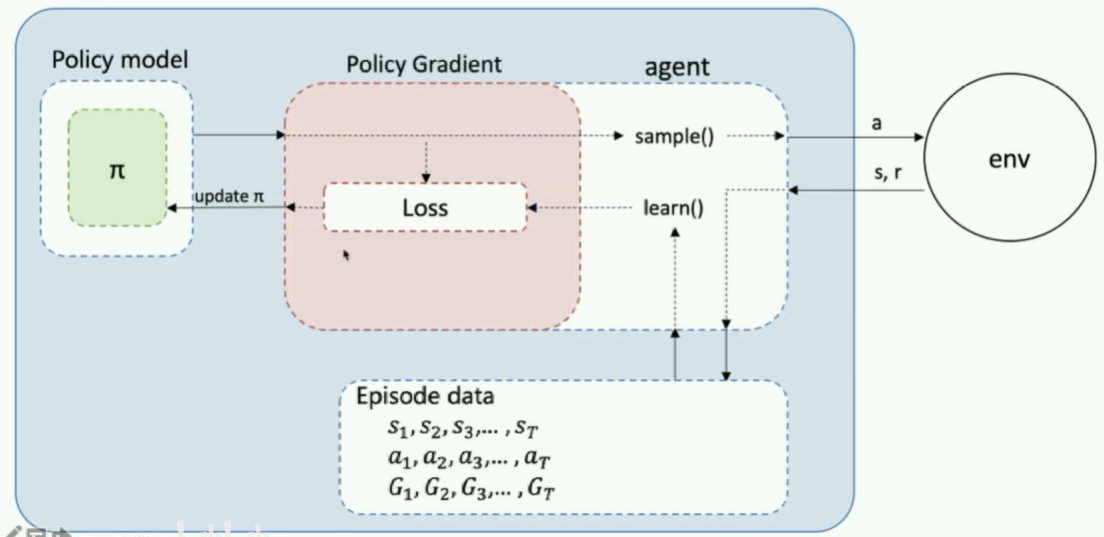
REINFORCE 框架图
- 分类:On-policy / Policy-based
- 输入:一个 Episode 的 序列、 序列和 序列
- 更新:
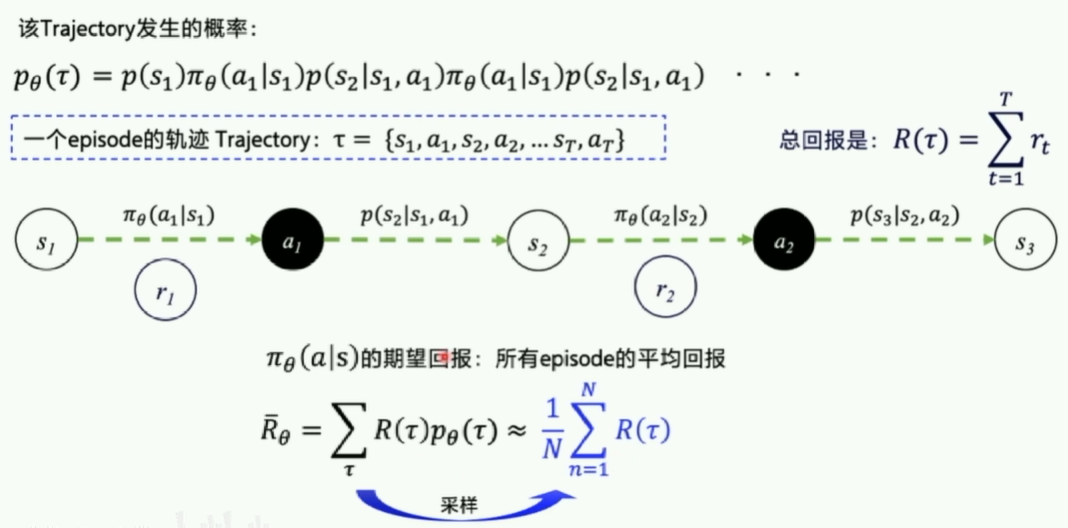
- 优化目标:最大化期望回报,梯度上升 其中
- 损失函数:
- 对于每个 action:
- 用交叉熵来理解:
- Log 项在计算神经网络的输出(动作概率)和实际动作(而不是正确动作;是一个 one-hot 向量,动作列表中实际动作位置为 1)之间的差距;
- 要乘以一个奖励回报,即对实际动作的评价,作为权重决定哪部分需要重点优化
- 用交叉熵来理解:
- 对于每次更新:
- 对于每个 action:
A2C (Advantage Actor-Critic)
核心思想
- 问题:
- 训练不稳定:
- REINFORCE 对实际动作评价时,直接使用 作为权重:
- 而 方差很大,导致训练不稳定
- 缺乏相对评价:无法区分“好结果是因为动作好”还是“环境本身奖励高”
- 解决:
- 优势函数(Advantage Function):
- 引入基线:减去一个基准值以减少方差:
- 定义 (状态价值函数)
- 衡量在状态 下执行动作 相比平均水平的”优势” 即超预期的部分
- 实际中常用 TD 误差近似:
- 引入 Critic:
- Actor(演员):策略网络 ,负责执行动作
- Critic(评论家):价值网络 ,估计状态价值,提供低方差基线
- 分类:On-policy / Policy-based
- 优势:
- 显著降低策略梯度方差,提升训练稳定性;
- TD 更新,无需等待 episode 结束;
- 为后续 A3C/PPO 等算法奠定 Actor-Critic 基础。
DDPG (Deep Deterministic Policy Gradient)
核心思想
- 问题:
- DQN 仅适用于离散动作空间,无法处理连续控制(如机器人关节力矩)
- REINFORCE/A2C 在连续空间中需输出概率分布,样本效率低且难以收敛
- 解决:
- 采用确定性策略:直接输出动作,而非概率,避免随机采样噪声
- 结合DQN 的稳定技巧:经验回放(off-policy) + 目标网络(soft update)
- Critic 使用 Q 函数评估动作价值
- 分类:Off-policy / Policy-based
- 更新:
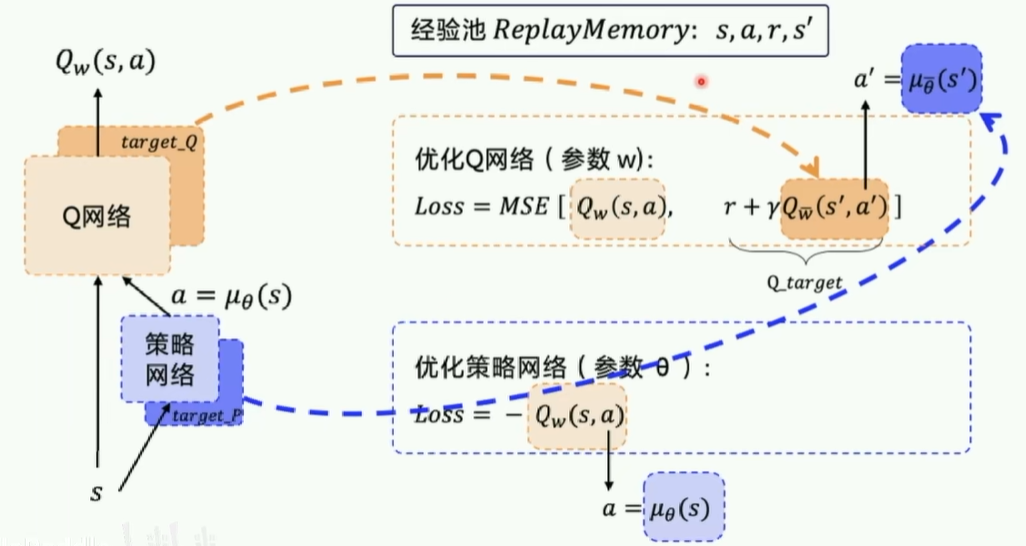
- Actor 更新:
- Critic 更新:
- 代码:
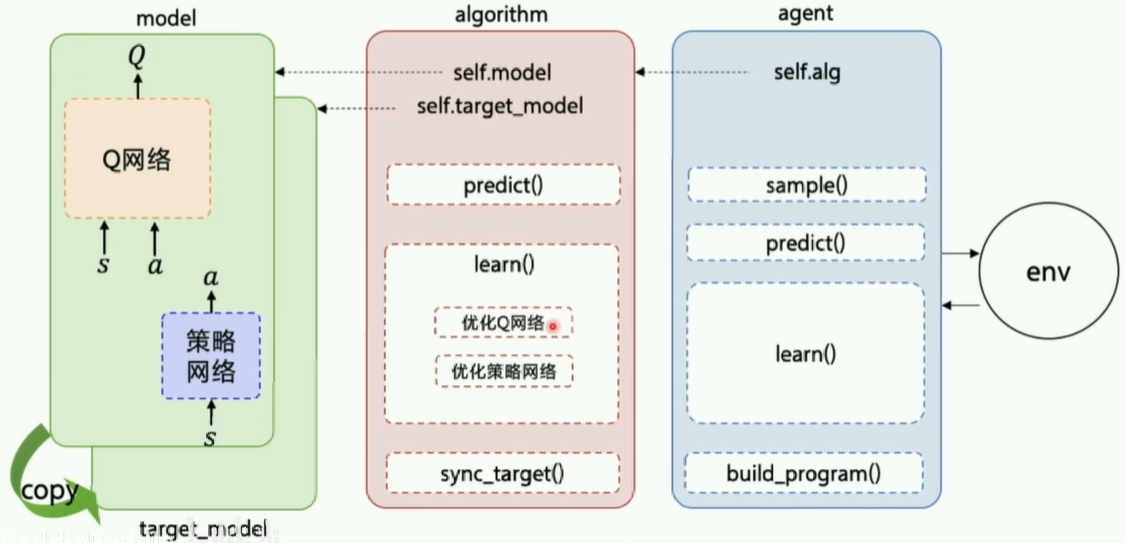
- Q 网络:
value() - 策略网络:
policy() - 优化 Q 网络:
_critic_learn() - 优化策略网络:
_actor_learn()
- Q 网络:
- 优势:
- 支持高维连续动作空间,适用于机械臂、自动驾驶等实际控制任务
- Off-policy 训练 + 经验回放,样本利用率高,数据效率优于 on-policy 方法
- 确定性策略输出平滑,更贴近经典控制理论中的控制律
A3C (Asynchronous Advantage Actor-Critic)
核心思想
- 问题:
- A2C(同步 A2C)依赖单一线程收集数据,样本相关性高、更新频率低
- On-policy 方法整体样本效率低,训练速度慢
- 解决:
- 异步并行架构:多个 worker 线程独立与环境交互,异步地从全局网络拉取参数、计算梯度、更新全局网络
- 每个 worker 使用 n-step TD 回报 估计优势函数,实现多步 bootstrapping
- 可选加入 熵正则项 鼓励探索,防止策略过早退化
- 分类:On-policy / Policy-based
- 更新:
- Actor 更新:
- Critic 更新:
- 熵正则化(可选):
- 优势:
- 天然去相关:多线程并行采样大幅降低数据相关性,提升梯度质量;
- 无需经验回放,内存占用低,适合 on-policy 场景;
- 训练速度快,在 Atari 等任务上首次实现纯 on-policy 方法的高效训练(虽然后续被 PPO 超越)
PPO (Proximal Policy Optimization)
核心思想
- 问题:
- On-policy 样本利用率低
- 策略更新步长难以控制:更新过大导致策略崩溃,过小则收敛慢。
- 解决:
- 引入重要性采样,允许对同一 batch 数据多次更新(有限重用)
- 裁剪目标函数,限制每次策略更新的幅度
- 分类:On-policy / Policy-based
- 更新:
- PPO-Clip 损失函数:
- 重要性采样权重:概率比,衡量新旧策略的差异
- 就是传统的策略梯度目标,用概率比加权优势函数
- 它对旧策略采样的样本进行加权调整,使其等效于“从新策略采样”
- 容易爆炸,导致高方差或偏差,需要限制范围
- 裁剪范围:(通常 0.1-0.2)
- 作用:保证不会过度更新/惩罚不会过度放大
- 价值函数损失:
- 熵正则化:鼓励探索,防止策略过早收敛
- 重要性采样权重:概率比,衡量新旧策略的差异
- PPO-Clip 损失函数:
- 算法变种:
- PPO-Clip(最常用):使用上述裁剪目标
- PPO-Penalty:在目标函数中添加 KL 散度惩罚项
- 优势:
- 训练极其稳定,对超参(如 )不敏感
- 样本效率较高(相对其它 On-Policy 方法)
- 实现简单、通用性强,适用于离散/连续动作、仿真/真实机器人等广泛场景